Home / Tutorials

Geographic Correlation Analysis With ArcGIS Online

One of the useful capabilities of GIS software is the ability to overlay multiple layers of data so you can observe where characteristics correlate with each other in space.

This tutorial will describe how to perform simple geographic correlation analysis with ArcGIS Online, and export data to Google Sheets for visualization. The example will use stroke incidence rates as the dependent variable and a variety of independent variables derived from stroke risk factors.

Literature Review

Introduction

Stroke is a disease that affects the arteries leading to and within the brain. A stroke occurs when a blood vessel that carries oxygen and nutrients to the brain is either blocked by a clot or ruptures, resulting in failure of parts of the brain to get needed oxygen, and death of brain cells. Around 800,000 people in the USA have a stroke each year, and around 130,000 Americans are killed by stroke, making stroke the fifth leading cause of death in the United States (American Stroke Association 2018a; 2018b).

The symptoms of stroke vary in severity based on the scale of the blockage or hemmorage, as well as the specific location in the brain where that event occurs. Symptoms of stroke can include (American Stroke Association 2018a):

Risk Factors

The risk factors for stroke are similar to those for heart disease, and stroke often has co-morbidity with other health conditions common in contemporary American life. Risk factors include (American Stroke Association 2018c):

Study Area

This research will focus on geographic correlates of stroke in the United States. While stroke is common throughout the country, there are especially high rates of stroke incidence in the "Stroke Belt," an area that encompasses a number of states of the old Confederacy in the southeast portion of the country (Wikipedia 2018).

Questions and Hypotheses

Given the association of many stroke risk factors with poverty (Cox et al. 2006), and the hypothesized physiological responses to the constraints imposed upon subordinated members of society (Neser, Tyroler, and Cassel 1971), our research question is: Do areas that have lower income also have higher stroke mortality?

Our hypothesis is that stroke mortality will be inversely correlated with median household income by state.

Methods and Data Sources

Independent variables were tested for bivariate spatial correlation with the dependent variable using least-squares regression in Google Sheets.

Our dependent variable is the stroke mortality among US adults (18+) per 100,000 population. The data is for 2016 from the Centers for Disease Control and Prevention's Chronic Disease Indicators.

Our independent variable for median household income is from the US Census Bureau's American Community Survey five-year estimates, 2013-2017.

Dependent and Independent Variable Choropleth

When analyzing causation, the causes are measured with independent variables and the effects are measured with dependent variables. Effects are dependent upon the independent causes.

A choropleth is a map in which area are shaded or patterned based on a variable. They are a common way of visualizing quantitative geospatial data.

For this tutorial, we use as an example dependent variable mortality from cerebrovascular disease (stroke) per 100,000 population for 2016 from the CDC's Chronic Disease Indicators.

This data was uploaded to an ArcGIS Online hosted feature layer and this video shows how to create a map of the stroke variable.

  1. Create a new map
  2. Click Add to search the appropriate content area to find the layer containing the variable you want to map and add that layer to the map
  3. Change Style and Choose an attribute to show with the variable for the condition you want to map
  4. Select a drawing style of Counts and Amounts (color) to create a choropleth, and configure the Options
  5. Select Symbols to change the color to the color of your choice. Red is used in this case because red is commonly associated in the West with bad things like disease
  6. If you use red, reverse the color ramp so the darker red is associated with higher levels
  7. Click OK and Done to accept your changes to the styling
  8. Save the map under a meaningful name. Because ArcGIS Online is a shared resource, map names must be unique in an organization. Using your name in the title will help keep the name unique in your organization so there is no naming conflict
  9. Share the map with Everyone (public) to get a URL link you can share
Mapping the Example Dependent Variable From an Existing Layer

Joining an Independent Variable Layer

While ArcGIS Online does not have a feature for creating X/Y scatter charts directly, we can create a layer containing all dependent and independent variables, export it to a CSV file, import it into Google Sheets, and create charts there.

However, we first must get all the variables into one layer.

If one of your variables is in an existing layer, you can perform a spatial join of the layer with the independent variable(s) to the layer with the dependent variable to get a combined layer.

For this example, we use a layer of median household income from the 2013-2017 American Community Survey five-year estimates.

  1. Add the layer that you will be joining to the map
  2. Click the Perform Analysis icon under the layer containing the dependent variable and select Summarize Data, Join Features
  3. The Target layer is the layer with the dependent variable, and the layer to join to the target layer is the layer with the independent variable(s)
  4. The type of join is Choose a spatial relationship, Identical to
  5. Give the layer a meaningful name
  6. Uncheck Use current map extent so that any features that are outside the current map view will also get joined
  7. Select Show credits to make sure your operation is reasonable. Joins over 5 credits should be examined to make sure you actually want to do what you are about to do
  8. Run Analysis
  9. This join may take a minute or two, although this tool has a tendency to complete without notifying the user (especially on Microsoft browsers). If you are waiting for more than two minutes, create a new map and find the joined layer
  10. Examine the attribute table of the resulting layer to make sure all attributes are there and look like you expect
  11. Turn off the other layers so that only your joined layer is visible
  12. Symbolize by the independent variable to make sure the joined data is what you expect
Joining Attributes From Another Layer

Joining an Independent Variable Layer via Centroids

When joining layers using polygons that are not exactly identical, such as from different years or different data sources, your join may fail by only joining a subset of polygons or none at all, resulting in the error, The result of your analysis did not return any features:

Failed Join

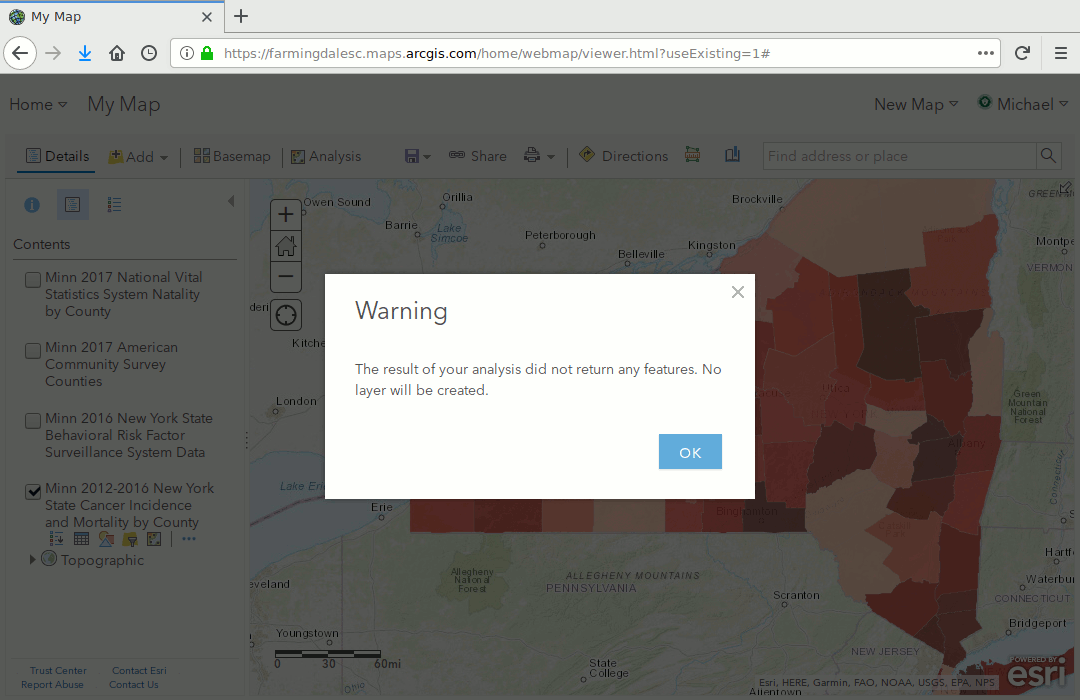
You can address this problem by first converting one of your layers to centroids (central points within the polygons), then joining the centroids that intersect the other set of polygons.

  1. Add the layer that you will be joining to the map
  2. Click the Perform Analysis icon under the layer containing the dependent variable and select Find Locations, Find Centroids
  3. Give the layer a meaningful name
  4. Run Analysis

The centroid points should appear in the center of the polygons you are joining. You can then perform a spatial join just as above.

  1. Click the Perform Analysis icon under the layer containing the dependent variable and select Summarize Data, Join Features
  2. The Target layer is the layer with the dependent variable, and the layer to join to the target layer is the layer with the independent variable(s)
  3. The type of join is Choose a spatial relationship, Intersects
  4. Give the layer a meaningful name
  5. Uncheck Use current map extent so that any features that are outside the current map view will also get joined
  6. Select Show credits to make sure your operation is reasonable. Joins over 5 credits should be examined to make sure you actually want to do what you are about to do
  7. Run Analysis
  8. This join may take a minute or two, although this tool has a tendency to complete without notifying the user (especially on Microsoft browsers). If you are waiting for more than two minutes, create a new map and find the joined layer
  9. Examine the attribute table of the resulting layer to make sure all attributes are there and look like you expect
  10. Turn off the other layers so that only your joined layer is visible
  11. Symbolize by the independent variable to make sure the joined data is what you expect
  12. Save As the map under an appropriate new title and Share
Joining Attributes From Another Layer Via Centroids

Export

To transfer your data to Google Sheets for visualization, you need to export the attributes of your combined layer to a CSV file, and then download that CSV file to your computer.

  1. View the item details for your layer containing your dependent and independent variables
  2. Select Export Data -> Export to CSV file
  3. When given the CSV file page, Download a zip archive of the CSV file
  4. Extract the CSV file from the zip archive and copy it to your desktop
CSV Download

Directory Cleanup

Store all files associated with this analysis in a separate directory so you can keep track of what files go with what project.

  1. Save and share your map
  2. On your Content page, create a new, meaningfully-named directory
  3. Delete any layers that were created during unsuccessful operations
  4. Move all files and maps associated with this analysis into that directory to keep everything organized
Project Directory Cleanup

Correlation Analysis: X/Y Scatter Chart

Correlation is "a relation existing between phenomena or things or between mathematical or statistical variables which tend to vary, be associated, or occur together in a way not expected on the basis of chance alone" (Merriam-Webster 2020).

R2 is the coefficient of determination that measures the strength of the correlation. The range is from 0.000 (no correlation) to 1.000 (perfect correlation).

Exactly how R2 should be evaluated depends on the type of data being studied. In the natural sciences, values above 0.600 are often expected. However, in the social sciences where relationships often involve the complex interplay of ambiguous factors, values in the 0.200s or 0.300s can be considered meaningful for further investigation.

To create an X/Y scatter chart in Google Sheets and find the R2:

  1. Create a new Google Sheets spreadsheet in Google Drive
  2. Import the CSV you downloaded from ArcGIS Online into your spreadsheet
  3. Give the spreadsheet a meaningful name
  4. Select two columns you want to compare (ctrl-click to select the second column)
  5. Insert, Chart to create a new chart with the two columns
  6. Add axis titles so you know what the chart shows
  7. Series, Add Trendline to add a trendline
  8. Adjust the color and thickness for the trendline as desired
  9. Display the R2 value to measure the strength of the correlation
  10. Move to own sheet
  11. Publish chart to get a Link (if you are sending a link to someone) or Embed an iframe (if you are embedding the chart in a web page)
Creating X/Y Scatter Charts with Google Sheets

Results

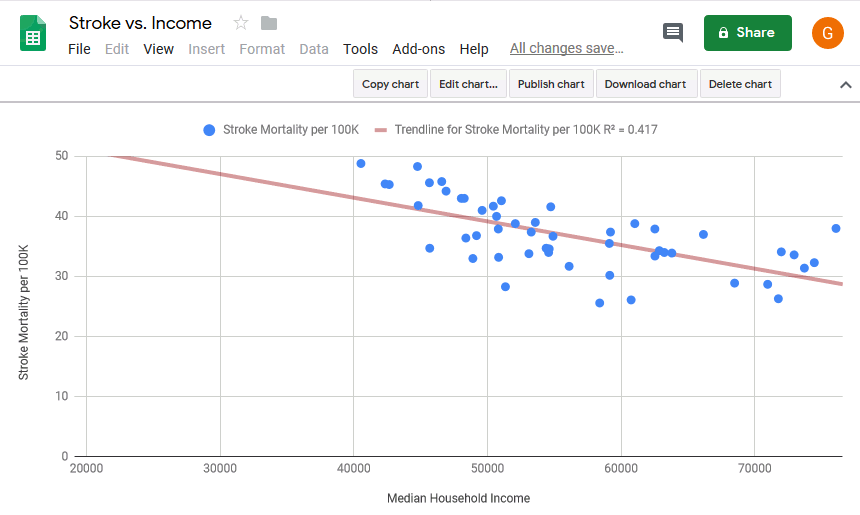
Median household income has a fairly strong inverse correlation with stroke mortality by state, with an R-squared of 0.417.

This corroborates our hypothesis that income would be inversely correlated with stroke mortality by state.

2016 Stroke Mortality in US States vs Median Household Income (CDC, USCB)

Limitations: Correlation vs. Causation

While correlation is interesting to people interested in data, we are usually more interested in causation, which refers to a cause-and-effect relationship between things. Once you understand a cause (or causes), you can change the effects by changing the causes.

For example, if you want to reduce rates of stroke death (effects) and find that lifestyle choices (causes) seem to be behind those higher rates of stroke deaths in a specific area, you can target that area with public health initiatives to increase awareness, change lifestyles, and, ultimately, reduce stroke deaths.

While correlation can be used to help find a cause or causes for some phenomena, correlation is a mathematical relationship that may or may not reflect a simple cause-and-effect relationship, resulting in the common adage correlation is not causation. Causes are almost always complex and require complex analysis to define and interpret.

Treating simple correlation as if it proves causation is an example of the post hoc fallacy. This fallacy is dangerous because it can lead to falsely assigning credit (or blame) for a positive (or negative) effect and lead to unnecessary, misleading, or dangerous actions that will do little to achieve the desired outcomes, and might even be counterproductive.

An example of the post hoc fallacy would be interpreting the the strong negative correlation between income and stroke mortality as saying that being poor will cause you to have a stroke. Being poor doesn't by itself cause strokes since there are many poor people who never have strokes, and many rich people who do. Low income is associated with a complex set of differences in healthcare, diet, and lifestyles that are associated with known risk factors for stroke (Cox et al. 2006).

Because correlation is not causation, and because the spatial analysis technique used in this tutorial is so weak, finding simple correlation does not prove a hypothesis. However, correlation can be evidence that a hypothesized relationship may exist. Therefore it is more accurate to say that a correlation corroborates a hypothesis rather than proves it.

Reference List

American Stroke Association. 2018a. "About Stroke." Accessed 30 September 2018. http://www.strokeassociation.org/STROKEORG/AboutStroke/About-Stroke_UCM_308529_SubHomePage.jsp.

American Stroke Association. 2018b. "Impact of Stroke (Stroke statistics)." Accessed 30 September 2018. http://www.strokeassociation.org/STROKEORG/AboutStroke/Impact-of-Stroke-Stroke-statistics_UCM_310728_Article.jsp.

American Stroke Association. 2018c. "Stroke Risk." Accessed 27 October 2018. http://www.strokeassociation.org/STROKEORG/AboutStroke/UnderstandingRisk/Understanding-Stroke-Risk_UCM_308539_SubHomePage.jsp.

Cox, Anna M., Christopher McKevitt, Anthony G. Rudd, and Charles DA Wolfe. 2006. "Socioeconomic status and stroke." The Lancet Neurology 5 (2): 181-188. https://www.sciencedirect.com/science/article/abs/pii/S1474442206703519.

Merriam-Webster. 2020. "Correlation." Accessed 14 April 2020. https://www.merriam-webster.com/dictionary/correlation.

Neser, W.B., H.A. Tyroler, and J.C. Cassel. 1971. "Social Disorganization and Stroke Mortality in the Black Population of North Carolina." American Journal of Epidemiology 93 (3): 166–175. https://academic.oup.com/aje/article-abstract/93/3/166/142806.

Wikipedia. 2018. "Stroke Belt." Accessed 30 September 2018. https://en.wikipedia.org/wiki/Stroke_Belt.