Home / Tutorials

BRFSS Data in R

The CDC's Behavioral Risk Factor Surveillance System (BRFSS) is a "system of health-related telephone surveys that collect state data about U.S. residents regarding their health-related risk behaviors, chronic health conditions, and use of preventive services." The BRFSS was initially established in 1984, and as of 2019 "completes more than 400,000 adult interviews each year, making it the largest continuously conducted health survey system in the world" (CDC 2019).

This tutorial demonstrates how to process and analyze anonymized survey responses in R.

Importing and Processing BRFSS Response Data

Download

Processed BRFSS data is made available in a variety of aggregations and settings. The raw, anonymized survey responses are made available as a fixed width column ASCII file from the CDC website..

Download and unzip the ASCII data file. The 2020 file used in this example was about 44 Mb zipped and 820 Mb unzipped, containing 401,958 rows and 279 columns.

BRFSS data on the CDC website

Variable Layout

The information on column positions is available as an HTML table, that you can copy into a CSV file. A version as a CSV is available here.

Variable layout table

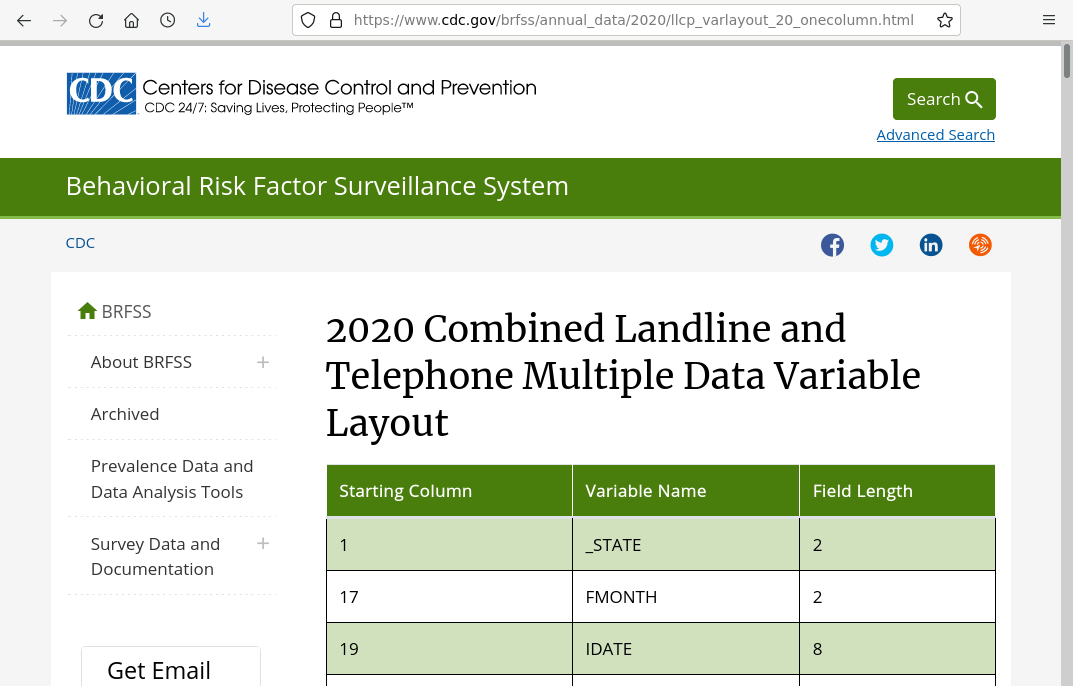
Note that the variable layout includes group fields that encompass multiple subsequent columns and have no independent width of their own (example: IDATE includes IMONTH, IDAY, and IYEAR). There are also blank columns between some fields. This code creates a data frame of columns that removes the group fields and calculates actual field widths in the file (File_Width) for each field, which will be needed to parse the file.

columns = read.csv("2020-column-layout.csv")

columns$File_Width = sapply(1:nrow(columns), function(y) ifelse(y < nrow(columns), 
	columns$Starting_Column[y + 1] - columns$Starting_Column[y], 1))

columns = columns[columns$File_Width > 0,]

Import File

Given the survey data .txt file and the field widths, you can use the read.fwf() function to import the data into a data frame. That function is a bit slow, and the call took around seven minutes for me. There are apparently faster functions like readr, but since this workflow involves copying out a subset into a new file, the extra effort may not be worth it unless you will be reading this file frequently.

Note that the trailing space in the file name is intentional since the file was apparently zipped with that trailing space.

responses = read.fwf("LLCP2020.ASC ", widths = columns$File_Width, col.names = columns$Variable_Name)

Select Columns

You will probably want to select and modify a specific subset of columns for your uses.

The CDC data page includes a codebook which describes the questions associated with each variable and the range / meaning of the field values.

BRFSS codebook

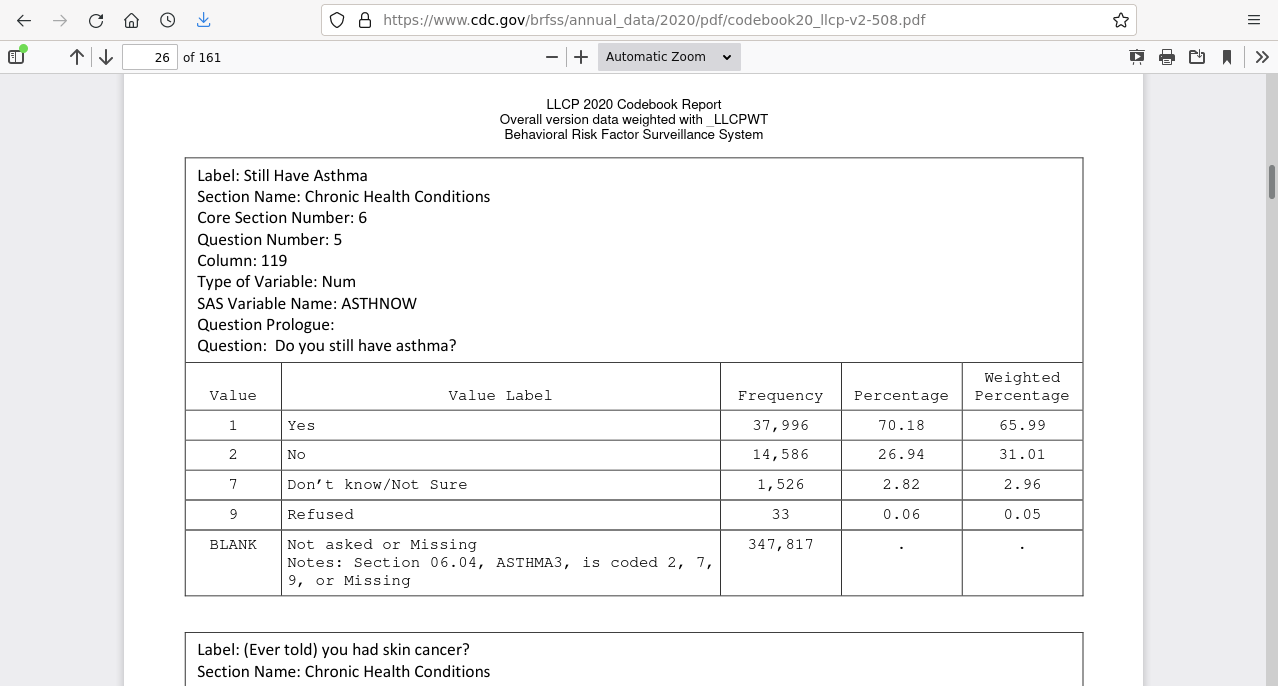
To make the response data more manageable, this code subsets a collection of notable columns with fairly consistent availability across all states.

name_list = c("X_STATE", "X_URBSTAT", "X_AGEG5YR", "DISPCODE", "NUMADULT", "SEXVAR", "GENHLTH",
"PHYSHLTH", "MENTHLTH", "HLTHPLN1", "EXERANY2", "SLEPTIM1", "CVDINFR4",
"CVDCRHD4", "CVDSTRK3", "ASTHMA3", "CHCSCNCR", "CHCOCNCR", "CHCCOPD2",
"HAVARTH4", "ADDEPEV3", "CHCKDNY2", "DIABETE4", "DIABAGE3", "LASTDEN4",
"RMVTETH4", "MARITAL", "EDUCA", "RENTHOM1", "VETERAN3", "EMPLOY1", "CHILDREN",
"INCOME2", "PREGNANT", "WEIGHT2", "HTIN4", "DEAF", "BLIND", "SMOKDAY2",
"STOPSMK2", "AVEDRNK3", "DRNK3GE5", "SEATBELT", "HADMAM", "PSATEST1",
"COLNSCPY", "HIVTST7", "HIVRISK5", "X_LLCPWT")

responses = responses[, name_list]

FIPS Codes

The only specific geospatial field in the data are FIPS (Federal Information Processing Standards) codes for states.

As a convenience, code adds a ST state abbreviation column based on the FIPS codes.

fips = read.csv("fips.csv")

colnames(responses)[colnames(responses) == "X_STATE"] = "FIPS"

responses = merge(fips[,c("FIPS", "ST")], responses, by = "FIPS", all.x=F, all.y=T)

Age Adjustment Weights

Risk for chronic health conditions tends to increase with age. When working with geospatial health data, incidence rates are commonly age-adjusted so that different areas can be compared more meaningfully regardless of whether they have unusually large concentrations of young or old residents (CDC 2021).

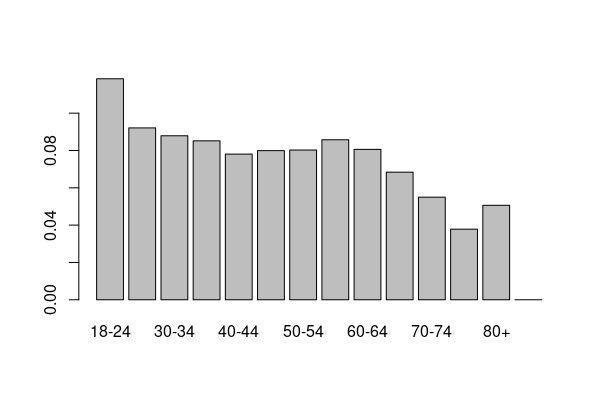
The CDC commonly age adjusts based on the proportion of five-year age groups (Klein and Schoenborn 2001). This code adapts 2019 population estimate proportions (USCB 2020) to get an age group weighting vector.

age.weights = c("18-24" = 0.118414, "25-29" = 0.09212, "30-34" = 0.087897,
	"35-39" = 0.085178, "40-44" = 0.078063, "45-49" = 0.079928, 
	"50-54" = 0.08024, "55-59" = 0.085726, "60-64" = 0.080608, 
	"65-69" = 0.068397, "70-74" = 0.05497, "75-79" = 0.037824, 
	"80+" = 0.050635, "No Response" = 0)

barplot(age.weights)
Five-year age group weightings based on 2019 US population estimates

As a convenience, this code adds an X_AAWEIGHT age-adjusted weighting column that is the product of the X_LLCPWT survey weighting column and the age group for each response. This variable can then be used for weighting when calculating age-adjusted means and proportions.

responses$X_AAWEIGHT = NA

for (state in na.omit(unique(responses$ST))) {
	state_rows = responses$ST %in% state

	groups = table(responses[state_rows, "X_AGEG5YR"])

	groups = groups / sum(groups)

	groups = age.weights[1:length(groups)] / groups

	responses[state_rows, "X_AAWEIGHT"] = 
		responses[state_rows, "X_LLCPWT"] *
		groups[responses[state_rows, "X_AGEG5YR"]]
}

Save CSV

Once you have processed the fixed-width file into a data frame that fits your needs, you may find it valuable to save that data frame to a CSV (comma-separated variable) file so you can save the processing time if you need the data in the future.

write.csv(responses, "2020-brfss-survey-responses.csv", row.names=F);

Import

A CSV file of 2020 data processed using the steps above is available for download here.

Tabular data can be read into a data frame using the read.csv() file. Data frames are analogous to spreadsheets with columns of data for variables arranged in rows.

responses = read.csv("2020-brfss-survey-responses.csv")

The dim() function shows the dimensions of the data frame in number of rows (survey responses in this example) and number of columns (variables on each response in this example).

dim(responses)

[1] 401958     49

The names() function shows the available variables. Consult the metadata (or the BRFSS codebook linked above) for documentation of what the variables represent and what the ranges of values are.

names(responses)

 [1] "FIPS"      "X_URBSTAT" "X_AGEG5YR" "DISPCODE"  "NUMADULT"  "SEXVAR"   
 [7] "GENHLTH"   "PHYSHLTH"  "MENTHLTH"  "HLTHPLN1"  "EXERANY2"  "SLEPTIM1" 
[13] "CVDINFR4"  "CVDCRHD4"  "CVDSTRK3"  "ASTHMA3"   "CHCSCNCR"  "CHCOCNCR" 
[19] "CHCCOPD2"  "HAVARTH4"  "ADDEPEV3"  "CHCKDNY2"  "DIABETE4"  "DIABAGE3" 
[25] "LASTDEN4"  "RMVTETH4"  "MARITAL"   "EDUCA"     "RENTHOM1"  "VETERAN3" 
[31] "EMPLOY1"   "CHILDREN"  "INCOME2"   "PREGNANT"  "WEIGHT2"   "HTIN4"    
[37] "DEAF"      "BLIND"     "SMOKDAY2"  "STOPSMK2"  "AVEDRNK3"  "DRNK3GE5" 
[43] "SEATBELT"  "HADMAM"    "PSATEST1"  "COLNSCPY"  "HIVTST7"   "HIVRISK5" 
[49] "ST"

Subsetting

Imported data will commonly contain missing values (NA) or special codes that need to be subsetted out in order to use the data meaningfully.

Data frames can be treated like arrays and subsets are taken by following the data frame name with square brackets.

For example, with the HTIN4 (height in inches) variable used in this example, the only cleaning needed will be removal of blank (NA) values:

height = responses[!is.na(responses$HTIN4),]

quantile(height$HTIN4, na.rm=T)

  0%  25%  50%  75% 100% 
  36   64   67   70   95

Special Codes

This particular BRFSS data set often mixes special codes in with quantitative values. Subsetting can remove those codes so you have only the quantitative values.

For example, the SLEPTIM1 (hours of sleep per 24-hour period) uses the values 77 for "Don't know/Not Sure" and 99 for "Refused," as well as NA (blank) if the data is not available.

sleep = responses[responses$SLEPTIM1 %in% 1:24, ]

quantile(sleep$SLEPTIM1)

  0%  25%  50%  75% 100% 
   1    6    7    8   24

WEIGHT2 (weight) is more complex, with codes for don't know / refused and specific ranges for respondents that answer in kilograms rather than pounds. The codes can be removed along with the NA values by subsetting values that are within the possible pound range of 50 to 776(!).

weight = responses[responses$WEIGHT2 %in% 50:776,]

quantile(weight$WEIGHT2)

  0%  25%  50%  75% 100% 
  50  150  175  205  758

For some variables, the code 88 is used for zero to more clearly separate nonzero values of interest. Those values can be selectively changed to zero with subsetting.

health = responses[responses$PHYSHLTH %in% c(1:30, 88),]

health[health$PHYSHLTH == 88, "PHYSHLTH"] = 0

quantile(health$PHYSHLTH, na.rm=T)

  0%  25%  50%  75% 100% 
   0    0    0    2   30

Distributions

A frequency distribution is "an arrangement of statistical data that exhibits the frequency of the occurrence of the values of a variable" (Merriam-Webster 2022).

The type of distribution will dictate what kinds of statistical techniques you should use on your data.

Frequency Tables

For categorical variables, the table() function can be used to tally frequency for each value in the distribution.

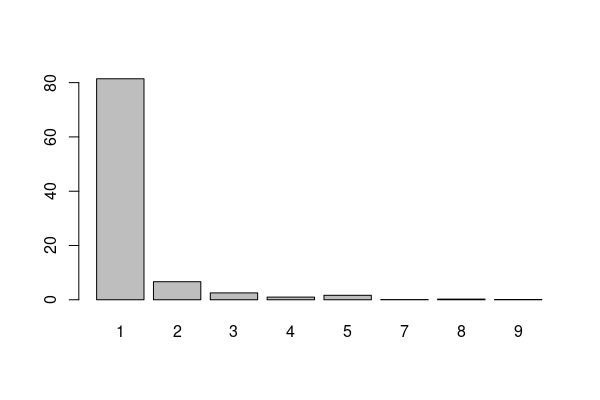
The mode for this distribution is clearly 1 (always wear a seat belt).

seatbelts = table(responses$SEATBELT, useNA="no")

print(seatbelts)

     1      2      3      4      5      7      8      9 
327249  26763  10195   3942   6632    263    976    427

Dividing the table by the number of responses and multiplying by 100 gives percentages that can be visualized as a bar graph with the barplot() function.

barplot(seatbelts * 100 / nrow(responses))
Seat belt usage Likert scale responses

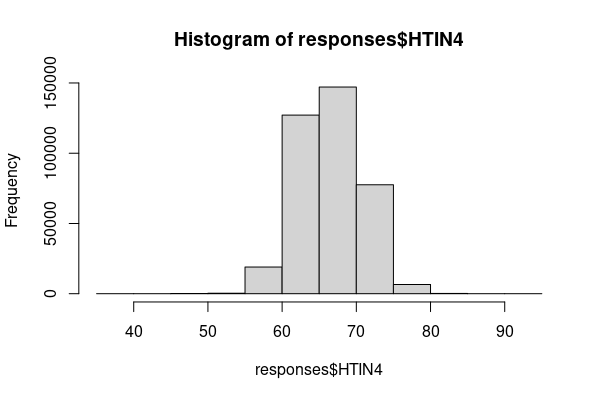
Histograms

For quantitative variables, a fundamental way of visualizing the frequency distribution is the histogram, which is a bar graph that shows the number of values within different ranges of values.

In R, the hist() function can be used to create a quick histogram. In this data, the HTIN4 variable is height in inches.

height = responses[!is.na(responses$HTIN4),]

hist(height$HTIN4)
Histogram of height in inches

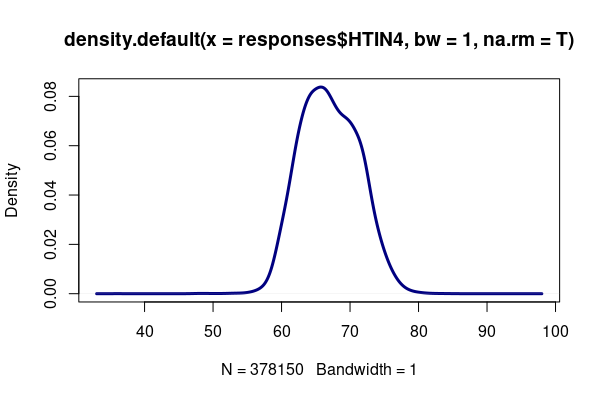
Density Plots

An alternative visualization to the histogram is a density plot that shows clearer detail by smoothing the histogram in manner similar to a continuous density distribution.

height = responses[!is.na(responses$HTIN4),]

plot(density(height$HTIN4, bw=1, na.rm=T), lwd=3, col="navy")
Density plot of height in inches

Normal Distributions

A normal distribution is an extremely common distribution in both the social and environmental sciences where data tends to cluster symmetrically around a central mean value with proportions of values decreasing as you move further above or below the mean. This distribution deserves special attention because many statistical techniques assumes variables that are normally distributed, and you should use caution in selecting analytical methods to make sure your method is appropriate for your distribution.

The frequency distribution curve for the normal distribution is often called the bell curve because of its bell-like shape. The density formula for that curve is a bit ugly:

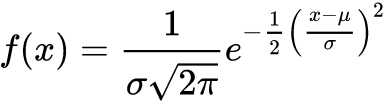
The general form of the normal probability density function (Wikipedia 2022)

R contains functions for analyzing and simulating a variety of distributions. The dnorm() function returns the density curve value for a specific value within the curve, and is used here to graph the normal curve:

plot(dnorm(seq(-4, 4, 0.1)), type="l", lwd=3, col="navy")
The normal curve

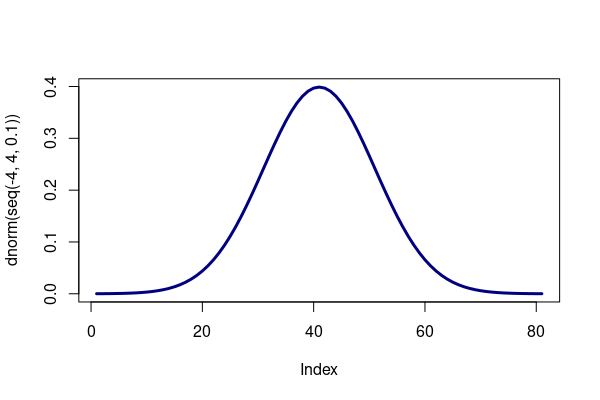
The height variable roughly follows a normal distribution, in which values tend to cluster around a central (mean) value, with fewer values as you get further above or below the mean.

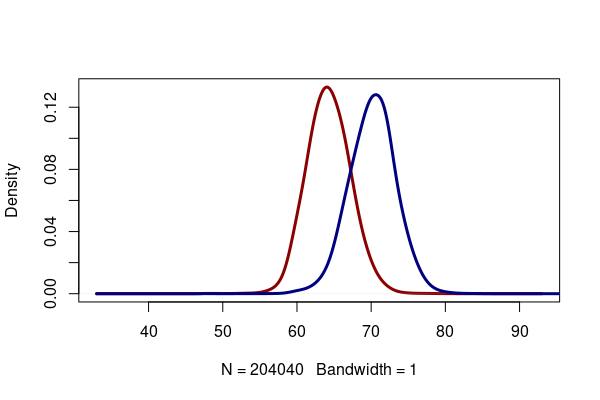
In the height density curve above, you may notice a slight notch on the right side of the curve. This is because men and women have separate normal distributions of height, and adding them together creates an asymmetrical curve.

height = responses[!is.na(responses$HTIN4),]

men = height[height$SEXVAR == "1", "HTIN4"]

women = height[height$SEXVAR == "2", "HTIN4"]

plot(density(women, bw=1, na.rm=T), lwd=3, col="darkred", main="")

lines(density(men, bw=1, na.rm=T), lwd=3, col="navy")
Separate density plots for men (blue) and women (red)

Skew

A normal distribution is symmetrical in that there are an equal number of values above and below a central value, and the values change in a similar manner as you move above or below that central value.

Skew occurs when the distribution contains values extend a greater distance from the mean either on the high (right skew) or low side (left skew).

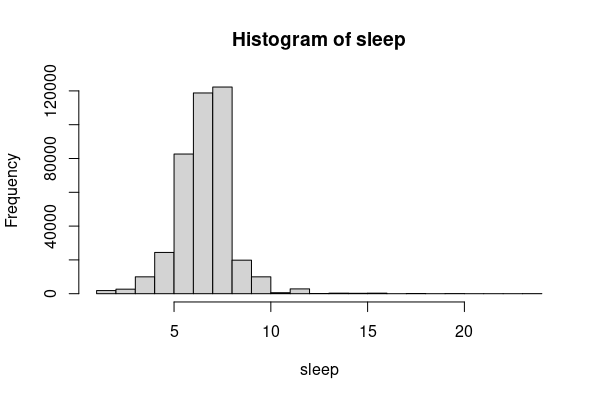
For example in this dataset, the number of hours that most people sleep per night is around seven hours per night, but there are a limited number of people who claim to sleep considerably more that, which skews the right tail of the curve far from the mean.

sleep = responses[responses$SLEPTIM1 %in% 1:24, ]

hist(sleep$SLEPTIM1)
Distribution of hours of sleep per night

Modality

The mode of a distribution is the most common value in the distribution. With quantitative variables, the mode is the peak of the density curve.

Distributions like the normal distribution are unimodal because they have one peak value around which a smaller number of higher and lower values cluster.

Multimodal distributions have more than one prominent peak value.

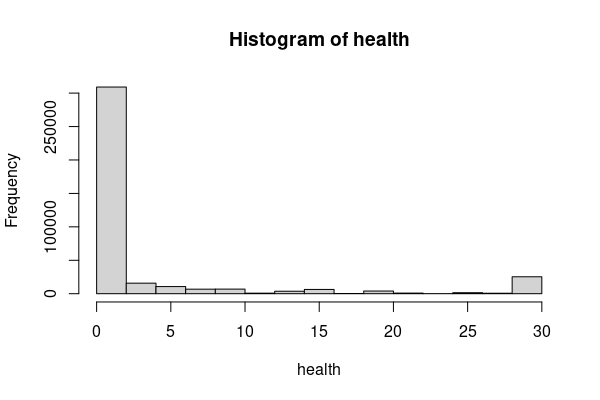
For example in this data, the number of days over the past 30 days that respondents indicated that they felt their physical health was not good clusters into two modes representing generally well people (zero on one day) and people with chronic illnesses (all 30 days).

health = responses[responses$PHYSHLTH %in% c(1:30, 88),]

health[health$PHYSHLTH == 88, "PHYSHLTH"] = 0

hist(health$PHYSHLTH)
Multimodal distribution of people by number of days over the past 30 days that felt their physical health was not good

Measures of Central Tendency

When working with a variable, we often wish to summarize the variable with a measure of central tendency, which is a single value that represents the center of the distribution.

There are three primary types of central tendency values: mean, median, and mode.

Mean

The arithmetic mean of a variable is the sum of all values divided by the number of values. In common parlance, arithmetic means are often simply called means or averages.

In R, the mean() function calculates the arithmetic mean of the vector or field passed to it. The na.rm=T parameter is often helpful since mean() will return NA if any values within the variable are NA, and na.rm=T instructs mean() to ignore NA values.

height = responses[!is.na(responses$HTIN4),]

plot(density(height$HTIN4, bw=1, na.rm=T), lwd=3, col="navy", main="")

x = mean(height$HTIN4, na.rm=T)

abline(v=x, col="darkred", lwd=3)

print(x)

[1] 66.99402
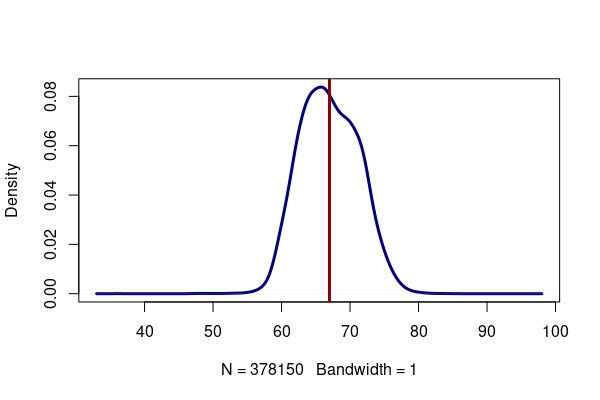
A density plot of height (in inches) with a line for the mean

Median

A median is a central tendency value where half of the values in the distribution are below the median and half are above the median.

Medians are often used rather than means with non-normal or heavily skewed distributions where outliers can make the mean unrepresentative of the phenomenon being summarized.

For example, if a billionaire developer walks into a room full of construction workers, the mean income will jump dramatically, while the median will stay largely the same and be more representative of the income of the people in the room.

In a symmetrical distribution like the normal distribution, the mean and median should be nearly identical.

In skewed distributions, the mean will be biased in the direction of the outliers. Whether that is undesirable depends on what you wish to convey in your analysis. For example, with the skewed distribution of sleep hours per night, the median is an even seven, which reflects the bulk of the responses. But the mean is slightly higher, which more-clearly communicates that there are some folks who get more than seven hours of sleep per night.

sleep = responses[responses$SLEPTIM1 %in% 1:24, ]

sleep.mean = mean(sleep$SLEPTIM1, na.rm=T)

sleep.median = median(sleep$SLEPTIM1, na.rm=T)

plot(density(sleep$SLEPTIM1, na.rm=T, bw=0.5), col="gray", lwd=3, main="")

abline(v=sleep.mean, col="navy", lwd=3)

abline(v=sleep.median, col="darkred", lwd=3)

legend("topright", lwd=3, lty=1, col=c("navy", "darkred"), legend=c("Mean", "Median"))

print(sleep.mean)

print(sleep.median)

[1]  7.097099

[1] 7
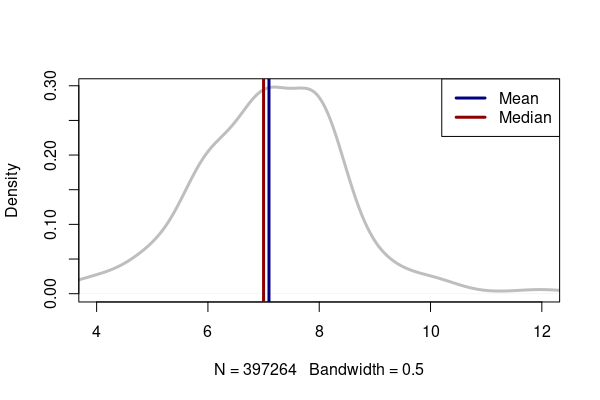
Mean vs. median hours of sleep per night

Mode

The mode of a distribution is the most common value in the distribution.

This concept is most clearly applicable categorical variables that have a limited number of possible values, such Likert scales that convert qualitative perspectives into ordinal quantitative values.

For example, the SEATBELT question is a Likert scale based on respondent ratings of their seatbelt usage on a scale of one (always) to five (never). Additional codes are included for people who were unsure, who never drive, or who refused to answer the question.

The table() function tallies frequency for each value in the distribution.

The mode for this distribution is clearly 1 (always wear a seat belt).

seatbelts = table(responses$SEATBELT)

print(seatbelts)

     1      2      3      4      5      7      8      9 
327249  26763  10195   3942   6632    263    976    427

Dividing the table by the number of responses and multiplying by 100 gives percentages that can be visualized as a bar graph with the barplot() function.

barplot(seatbelts * 100 / nrow(responses))
Seat belt usage Likert scale responses

While this visualization shows a clear dominance of people who respond that they always wear seat belts, keep in mind that with responses that involve politically-sensitive issues or imply a moral judgment, people often exhibit social desirability bias.

Bias is "systematic error introduced into sampling or testing by selecting or encouraging one outcome or answer over others" (Merriam-Webster 2022).

Social desirability bias is a problem with surveys in which participants (intentionally or unintentionally) respond with the answer they think they are supposed to give rather than an answer that accurately reflects what they actually do in their lives (Krumpal 2013).

Measures of Variation

In order to fully describe a distribution you need not only a central value, but a measure of how the values in a distribution vary across the range of values.

Range

The simplest measure of variation with a quantitative value is the range() of values.

Note that ranges tell you nothing about the frequency of values, so outliers can cause range to give a distorted picture of what the data actually shows.

height = responses[!is.na(responses$HTIN4),]

range(height$HTIN4, na.rm=T)

[1] 36 95

For categorical variables, the unique() function shows all possible values. 

unique(responses$MARITAL)

[1]  3  1  2  4  5  9  6 NA

Percentiles

A percentile is "a value on a scale of 100 that indicates the percent of a distribution that is equal to or below it" (Merriam-Webster 2022).

Percentiles can be calculated by passing a probability in the prob parameter of the quantile() function.

For example, this code uses the quantile() function to calculates the 25th percentile of height, which means that 25% of male respondents were at or below 68 inches in height.

height = responses[!is.na(responses$HTIN4),]

men = height[height$SEXVAR %in% 1, ]

quantile(men$HTIN4, prob=0.25)

25% 
 68

Going the other direction and asking what percent of respondents meet a condition requires a bit of calculation based on the number of rows in a subset that meet that condition, divided by the total number of rows, and multiplied by 100 to get a percentage.

over.six.feet = 100 * sum(men$HTIN4 > 72) / nrow(men)

paste0(round(over.six.feet,2) , "% of male respondents are over 6 feet tall.")

[1] "20.07% of male respondents are over 6 feet tall."

Quantiles

A quantile is a set of values that divide a frequency distribution into classes (bins) that each contain the same percentage of the total population.

The values dividing bins are percentiles. Quantiles are especially useful for describing non-normal distributions.

Quantiles with commonly used numbers of classes have their own names. A quartile is three percentile values that divide a distribution into four groups. A quintile is four percentile values that divide a distribution into five groups.

The quantile() function can display quantile values for a variable. By default, the quantiles are displayed in 25% percentile intervals with the 0% percentile being the lowest value in the range, the 50% percentile being the median, and the 100% percentile being the highest value in the range.

height = responses[!is.na(responses$HTIN4),]

quantile(height$HTIN4)

  0%  25%  50%  75% 100% 
  36   64   67   70   95

A barplot() can be used to visualize a quantile(), although such graphics can be confused with histograms.

barplot(quantile(height$HTIN4))
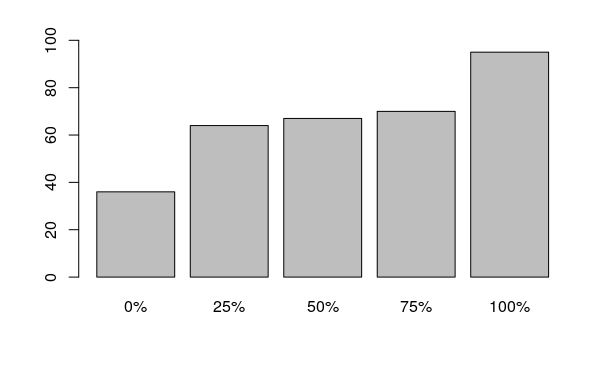
A bar plot of quantile values for height from the BRFSS

Quantiles comparing different groups are commonly visualized as side-by-side box-and-whisker plots using the boxplot() functions. By default, box-and-whisker plots in R represent the following values (Ford 2015).

height = responses[!is.na(responses$HTIN4) & !is.na(responses$SEXVAR),]

boxplot(HTIN4 ~ SEXVAR, data = height)

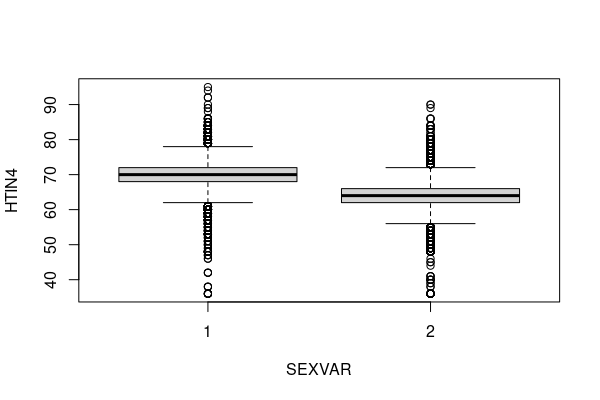
Standard Deviation

With normally-distributed data, the width of the bell curve is specified by the standard deviation. Standard deviation is represented by the lower-case Greek letter sigma (σ), which looks like a lower-case English "b" that's had too much to drink. Standard deviation for discrete values is calculated as the square root of the sums of the squares of deviations of the values (xi) from the mean (μ).

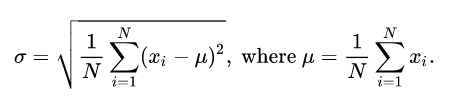
Formula for standard deviation (Wikipedia 2020)

The number of standard deviations that a value departs from the mean is called the z-score. The z-score of the mean is zero.

Converting values to z-scores is called standardizing, which allows comparison between values from different distributions.

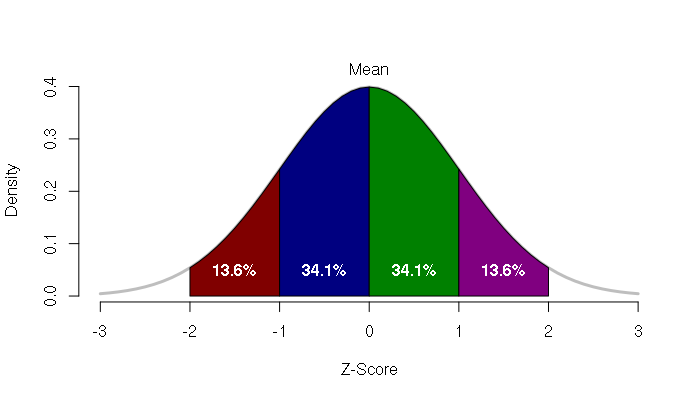
The area under the bell curve between a pair of z-scores gives the percentage of things associated with that range range of values. For example, the area between one standard deviation below the mean and one standard deviation above the mean represents around 68.2 percent of the values.

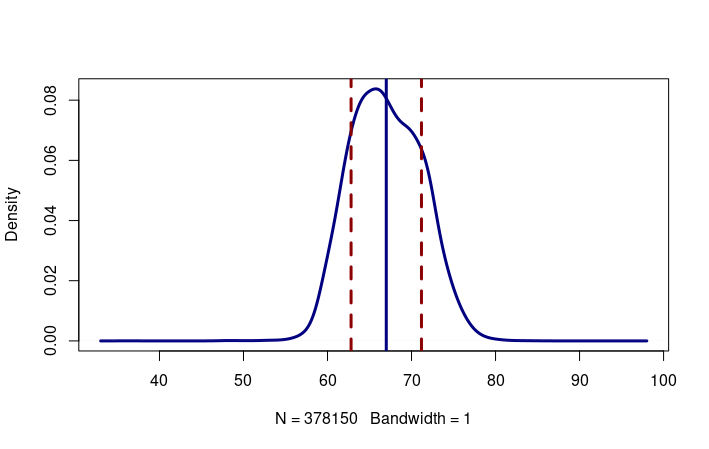
Percentages of Values Within A Normal Distribution

The sd() function can be used to calculate the standard deviation for a set of values. For example, this plots the density curve for height, along with vertical lines for the mean, one standard deviation below the mean (z = -1) and one standard deviation above the mean (z = 1).

height = responses[!is.na(responses$HTIN4),]

height.mean = mean(height$HTIN4, na.rm=T)

height.sd = sd(height$HTIN4, na.rm=T)

plot(density(height$HTIN4, bw=1, na.rm=T), lwd=3, col="navy", main="")

abline(v=height.mean, col="navy", lwd=3)

abline(v=height.mean - height.sd, col="darkred", lty=2, lwd=3)

abline(v=height.mean + height.sd, col="darkred", lty=2, lwd=3)

paste("The mean US height is", height.mean, 
	"inches with a standard deviation of",
	height.sd, "inches.")

The mean US height is 66.99402 inches with a standard deviation of 4.188529 inches.
Height density plot with means and standard deviations

Coefficient of Variation

One challenge with the standard deviation is that it is an absolute value that needs to be assessed in the context of the mean, which makes it difficult to compare the standard deviations for two different distributions.

One solution is to use the coefficient of variation. The coefficient of variation is the standard deviation divided by the mean, which gives a value that represents a percentage variation.

For example, with our height data, the coefficient of variation for women is slightly higher than that for men, which indicates that women's heights vary slightly more than men's heights.

height = responses[!is.na(responses$HTIN4),]

height.men = height[height$SEXVAR == 1,]

height.women = height[height$SEXVAR == 2,]

covar.men = sd(height.men$HTIN4) / mean(height.men$HTIN4)

covar.women = sd(height.women$HTIN4) / mean(height.women$HTIN4)

paste0("Coefficient of variation: men = ", 
	round(100 * covar.men, 2), 
	"%, women = ", 
	round(100 * covar.women, 2), "%")

[1] "Covariance: men = 4.42%, women = 4.51%"

Skew and Kurtosis

Skew is the extent to which values are evenly distributed around the mean. The skewness() function from the e1071 library can be used to calculate a value that will be negative if the left tail of the distribution is longer, and positive if the right tail of the distribution is longer. The skewness of a normal distribution is zero.

Kurtosis is a measurement of how flat or peaked the distribution is. The kurtosis() function from the e1071 library can be used to calculate a value that is positive for a sharply peaked distribution and negative for a distribution that is flatter than a normal distribution. The kurtosis of a normal distribution is zero.

For the example skewed distribution of hours of sleep per night, the positive skewness() corresponds to the long right tail and the high kurtosis() corresponds to the sharp peak around seven hours / night.

library(e1071)

sleep = responses[responses$SLEPTIM1 %in% 1:24,]

print(skewness(sleep$SLEPTIM1))

print(kurtosis(sleep$SLEPTIM1))

[1] 0.7551364

[1] 8.574684

In contrast, the largely normal distribution for height has very small values of both skewness and kurtosis.

height = responses[!is.na(responses$HTIN4),]

print(skewness(height$HTIN4))

print(kurtosis(height$HTIN4))

[1] 0.08109344

[1] -0.08372729

Weighting

The downloadable BRFSS data is raw, anonymized survey data that needs to be weighted because it is biased by uneven geographic coverage of survey administration (noncoverage) and lack of responsiveness from some segments of the population (nonresponse).

The X_LLCPWT field (landline, cellphone weighting) is a weighting factor added by the CDC that can be assigned to each response to compensate for these biases. See Weighting the BRFSS Data (CDC 2020) for more details on the calculation of these weighting factors.

X_LLCPWT can be used for weighting when calculating crude means and proportions at the state or national level.

The X_AAWEIGHT field is an age-adjusted weighting field (created above) that can be used for calculating age-adjusted means and proportions at the state or national level.

Weighted Means

The BRFSS data contains a handful of quantitative variables, although some assess comparatively rare behaviors or conditions that result in highly skewed distributions. In addition, some fields add special codes or ranges that need to be handled.

In these examples:

HTIN4 (height in inches) has no special codes and can be used after removing NA values and NA weights.

height = responses[!is.na(responses$HTIN4) & !is.na(responses$X_AAWEIGHT),]

height.raw = mean(height$HTIN4)

height.crude = weighted.mean(height$HTIN4, height$X_LLCPWT)

height.age.adjusted = weighted.mean(height$HTIN4, height$X_AAWEIGHT)

print(height.raw)

print(height.crude)

print(height.age.adjusted)

[1] 67.02791
[1] 67.04312
[1] 67.20037

WEIGHT2 (weight) is more complex, with codes for don't know / refused and specific ranges for respondents that answer in kilograms rather than pounds. The codes can be removed along with the NA values by subsetting values under the maximum pound range of 776(!).

weight = responses[(responses$WEIGHT2 %in% 50:776) & !is.na(responses$X_AAWEIGHT),]

weight.raw = mean(weight$WEIGHT2)

weight.crude = weighted.mean(weight$WEIGHT2, weight$X_LLCPWT)

weight.age.adjusted = weighted.mean(weight$WEIGHT2, weight$X_AAWEIGHT)

print(weight.raw)

print(weight.crude)

print(weight.age.adjusted)

[1] 181.7209
[1] 181.0673
[1] 180.6846

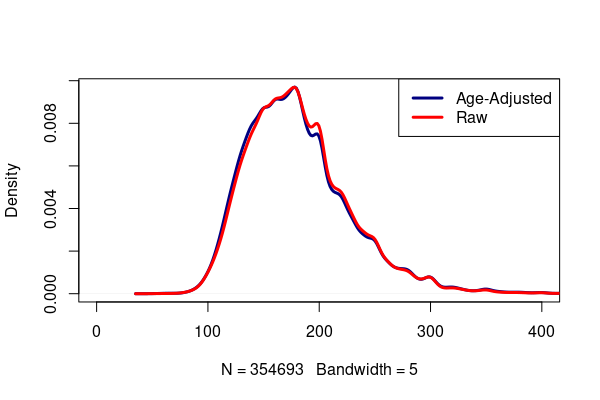
A comparative density plot shows the age adjusted body weight distribution shifted slightly lower than the distribution of raw samples.

plot(density(weight$WEIGHT2, weights=weight$X_AAWEIGHT / 
	sum(weight$X_AAWEIGHT), bw=5), lwd=3, col="navy", 
	xlim=c(0,400), main="")

lines(density(weight$WEIGHT2, bw=5), lwd=3, col="red")

legend("topright", lwd=3, col=c("navy", "red"), legend=c("Age-Adjusted", "Raw"))
Raw vs. age-adjusted national weight density curve

Weighted Mean MOE

Because the BRFSS is a sample, there is a margin of error associated with means. By using the wtd.var() function from the Hmisc library, we can calculate a weighted standard deviation and use that to calculate the 95% confidence interval.

library(Hmisc)

height = responses[!is.na(responses$HTIN4) & !is.na(responses$X_LLCPWT),]

height.mean = weighted.mean(height$HTIN4, height$X_LLCPWT)

height.sd = sqrt(wtd.var(height$HTIN4, height$X_LLCPWT))

height.stderr = height.sd / sqrt(nrow(height))

height.moe = 1.96 * height.stderr

paste("The mean height is", 
	round(height.mean, 2), "±", 
	round(height.moe, 2), "inches")

[1] "The mean height is 67.05 ± 0.01 inches"

Weighted Proportions

Proportions of responses to categorical questions can be weighted by summing the weights in the different categories and dividing by the overall sum of the weights. Multiplying by 100 gives values displayed as percents.

This code shows the crude national rate for heart attacks of around 4.2%. One is yes, two is no, seven is don't know, and nine is no response.

library(weights)

heart.percent = wpct(responses$CVDINFR4, responses$X_LLCPWT)

print(round(100 * heart.percent, 2))

    1     2     7     9 
 4.20 95.23  0.49  0.08

We can subset the responses to get a specific state.

heart = responses[responses$ST %in% "IL",]

heart.il = wpct(heart$CVDINFR4, heart$X_LLCPWT)

print(round(100 * heart.il, 2))

    1     2     7     9 
 3.90 95.69  0.26  0.15

By using the X_AAWEIGHT age-adjusted weighting parameter, we can get an age-adjusted rate. Illinois has median age slightly above the US median, which may account for an age-adjusted heart attack rate lower than the crude heart attack rate.

heart = responses[responses$ST %in% "IL",]

heart.il = wpct(heart$CVDINFR4, heart$X_AAWEIGHT)

print(round(100 * heart.il, 2))

    1     2     7     9 
 3.19 96.41  0.24  0.16

Weighted Proportion MOE

Using the general formula for proportions, we can find the margin of error.

heart.attack = heart.il[1]

heart.stderr = sqrt(heart.attack * (1 - heart.attack) / nrow(heart))

heart.moe = 1.96 * heart.stderr

paste(round(heart.attack * 100, 2), "±",
        round(100 * heart.moe, 2),
        "percent of IL residents have had heart attacks.")

[1] "3.19 ± 0.57 percent of IL residents have had heart attacks."

Weighted Likert Scales

A Likert scale is a technique commonly used on surveys to scale qualitative responses into ordinal values. Likert scale responses can be treated both as quantitative and categorical variables, although you will need to remove the special codes to get means.

For example, the GENHLTH variable is based on the question, "Would you say that in general your health is..." and respondents can then rank on a scale of one (excellent) to five (poor), with seven for don't know and nine for refused to answer.

library(weights)

health = responses[responses$ST %in% "IL",]

percents = wpct(health$GENHLTH, health$X_AAWEIGHT)

print(round(percents * 100, 1))

barplot(percents * 100)

   1    2    3    4    5    7    9 
24.2 35.0 28.7  9.2  2.7  0.1  0.0
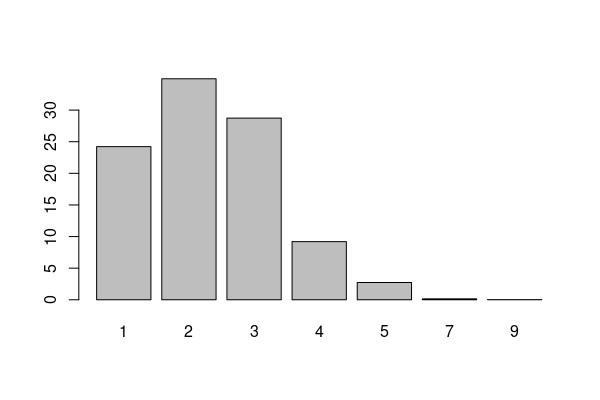
2020 Illinois general health Likert scale bar plot

To take a mean of a Likert scale, you should remove or transform the special codes.

health = responses[(responses$GENHLTH %in% 1:5) & !is.na(responses$X_AAWEIGHT),]

health = health[health$ST %in% "IL",]

health.age.adjusted = weighted.mean(health$GENHLTH, health$X_AAWEIGHT)

print(health.age.adjusted)

[1] 2.311411

Weighted Contingency Tables

Contingency tables can be used to detect relationships between categorical variables.

For this example we use SMOKDAY2 (current or former smoker) and CVDINFR4 (heart attack). Note that people who have never smoked have SMOKDAY2 as NA.

smoke = responses[!is.na(responses$X_AAWEIGHT) & 
	!is.na(responses$CVDINFR4) &
	!is.na(responses$SMOKDAY2),]

smoke = aggregate(smoke$X_AAWEIGHT, by=list(Smoker = smoke$SMOKDAY2, Heart.Attack = smoke$CVDINFR4), FUN=sum)

names(smoke)[3] = "Percent"

smoke$Percent = round(100 * smoke$Percent / sum(smoke$Percent), 2)

smoke = reshape(smoke, timevar="Smoker", idvar="Heart.Attack", direction="wide")

names(smoke) = c("Heart.Attack", "Daily", "Some Days", "Never", "Don't Know", "Refused")

print(smoke)

   Heart.Attack Daily Some Days Never Don't Know Refused
1             1  1.51      0.51  3.34       0.00    0.01
6             2 26.93     12.10 54.80       0.08    0.16
11            7  0.18      0.06  0.28       0.00    0.00
16            9  0.01      0.00  0.03         NA    0.00

Maps

Mapping Means

Aggregate means " to collect or gather into a mass or whole" (Merriam-Webster 2022).

The aggregate() function can be used to aggregate values by geographic areas.

weight = responses[(responses$WEIGHT2 %in% 50:776) & !is.na(responses$X_AAWEIGHT),]

weight$WEIGHT.SUM = weight$WEIGHT2 * weight$X_AAWEIGHT

weight.states = aggregate(weight[,c("WEIGHT.SUM", "X_AAWEIGHT")], by=list(ST = weight$ST), FUN=sum)

weight.states$AVGWEIGHT = weight.states$WEIGHT.SUM / weight.states$X_AAWEIGHT

weight.states = weight.states[order(weight.states$AVGWEIGHT),]

head(weight.states)

   ST WEIGHT.SUM X_AAWEIGHT  AVGWEIGHT
12 HI  193820169  1147803.9  168.8617
8  DC  117999411   690173.2  170.9707
20 MA  917219772  5297312.6  173.1481
35 NY 2610813502 15026814.8  173.7436
6  CO  806333502  4628338.2  174.2166
32 NJ 1116181092  6387053.7  174.7568

In order to map the aggregated data, we need to join the table data to geospatial polygons that indicate where to draw the features.

A join is an operation where two data frames are combined based on common key values.

Join

For this state-level data, we can use a GeoJSON file created with US Census Bureau polygons and ACS data that is available for download here.

library(sf)

states = st_read("2015-2019-acs-states.geojson")

states = states[!(states$ST %in% c("AK", "HI")),]

states = st_transform(states, 6580)

states.weight= merge(states, weight.states[,c("ST","AVGWEIGHT")])

palette = colorRampPalette(c("navy", "gray", "red"))

plot(states.weight["AVGWEIGHT"], breaks="quantile", pal=palette)
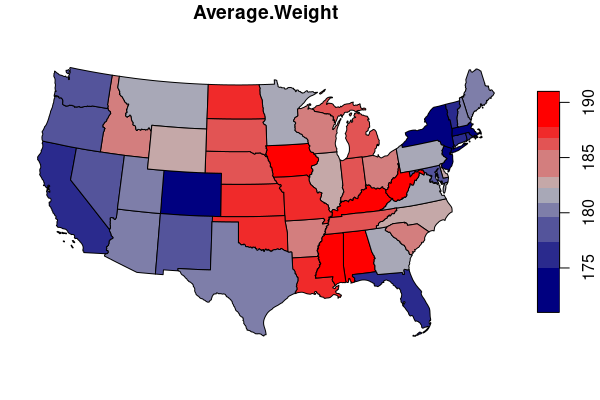
2020 BRFSS age-adjusted mean weight by state

Mapping Proportions

For categorical variables, the most straighforward visualization will be a map of the percentage of one of the categories.

To calculate state-level proportions, first aggregate a table of sums of weights for the selected values, then divide by the sum of the weights to get a weighted proportion.

For this example, we get a weighted percent of respondents who have answered yes (1) to the question, "Ever told you had a heart attack, also called a myocardial infarction?

heart = responses[!is.na(responses$X_AAWEIGHT),]

heart$HEART.SUM = ifelse(heart$CVDINFR4 %in% 1, heart$X_AAWEIGHT, 0)

heart.states = aggregate(heart[,c("HEART.SUM", "X_AAWEIGHT")], by=list(ST = heart$ST), FUN=sum)

heart.states$HEART.ATTACK = 100 * heart.states$HEART.SUM / heart.states$X_AAWEIGHT

heart.states = heart.states[order(heart.states$HEART.ATTACK),]

head(heart.states)

   ST HEART.SUM X_AAWEIGHT Heart.Attacks
8  DC  10365.90   768709.9      1.348480
31 NH  30773.18  1620881.6      1.898546
12 HI  25119.16  1202235.3      2.089371
7  CT  69825.33  3295819.6      2.118603
29 ND  17334.65   808834.5      2.143164
48 WA 154142.18  7009006.9      2.199201

library(sf)

states = st_read("2015-2019-acs-states.geojson")

states = states[!(states$ST %in% c("AK", "HI")),]

states = st_transform(states, 6580)

states.heart = merge(states, heart.states[,c("ST","HEART.ATTACK")])

palette = colorRampPalette(c("navy", "gray", "red"))

plot(states.heart["HEART.ATTACK"], breaks="quantile", pal=palette)
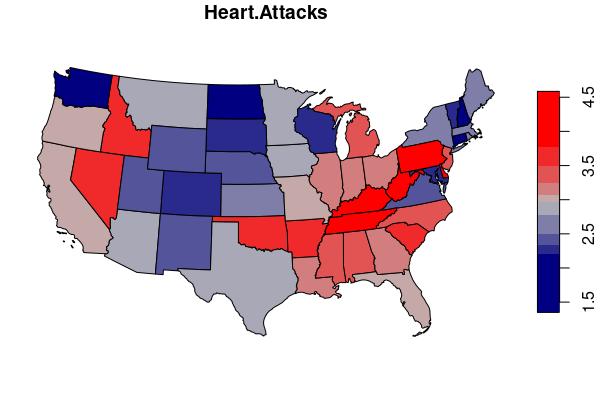
2020 BRFSS age-adjusted percentage of population by state that has had a heart attack

Classification

The choice of what colors to use for maps and what values to associate with those colors is both an aesthetic decision and a determinant of how readers will interpret a map.

With thematic choropleth maps like those used above, classification is the technique used to associate ranges of values with specific colors from the color palette used on the map. Classification choices are critical to the "story" a map will tell, and can be used to "lie" with maps (Monmonier 2018). Far from being objective representations of reality, maps incorporate numerous cartographic choices that reflect the subjectivities and goals of the cartographer.

With the plot() function from the sf library, the breaks parameter can be used to specify the algorithm for choosing the breaks between ranges of values associated with each color. The choice of algorithm will be influenced by the type of distribution. Some of the many options include:

par(mfrow=c(2,2))

palette = colorRampPalette(c("navy", "lightgray", "red"))

plot(states.heart["HEART.ATTACK"], pal=palette, breaks="fisher", main="Fisher-Jenks")

plot(states.heart["HEART.ATTACK"], pal=palette, breaks="quantile", main="Quantile")

plot(states.heart["HEART.ATTACK"], pal=palette, breaks="sd", main="Standard Deviation")

plot(states.heart["HEART.ATTACK"], pal=palette, breaks="equal", main="Equal Interval")
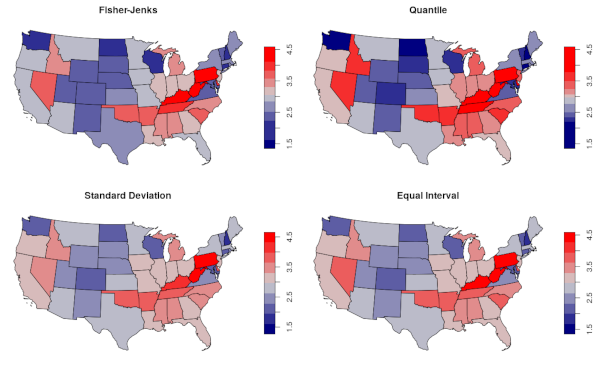
Comparison of different classification algorithms with percent of people who have had heart attacks by state

Modifiable Areal Unit Problem

Different choices of what types and boundaries of areas you used to aggregate spatial data can result in radically different results.

The modifiable areal unit problem

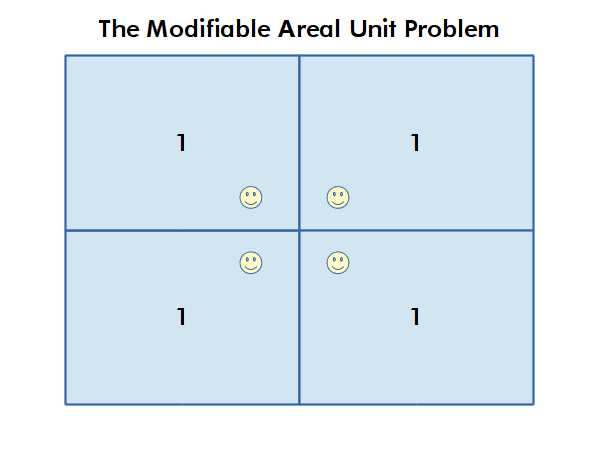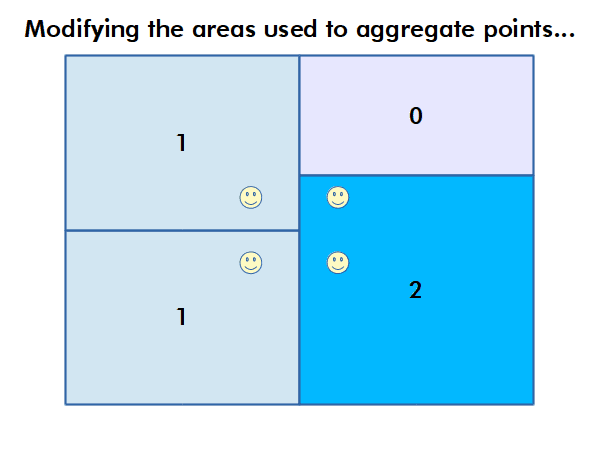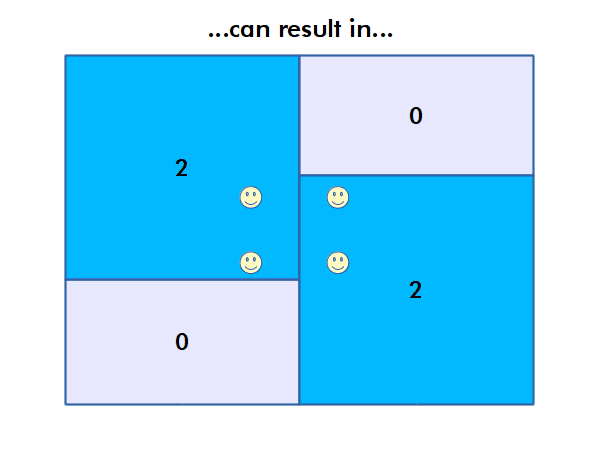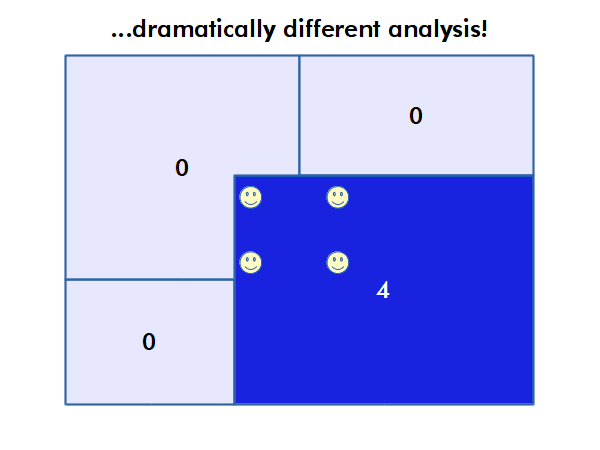
The modifiable areal unit problem (MAUP) is "a source of statistical bias that is common in spatially aggregated data, or data grouped into regions or districts where only summary statistics are produced within each district, especially where the districts chosen are not suitable for the data" (wiki.gis.com 2022).

For example, maps of electoral results give a very different impression depending on whether you map by state or by county.

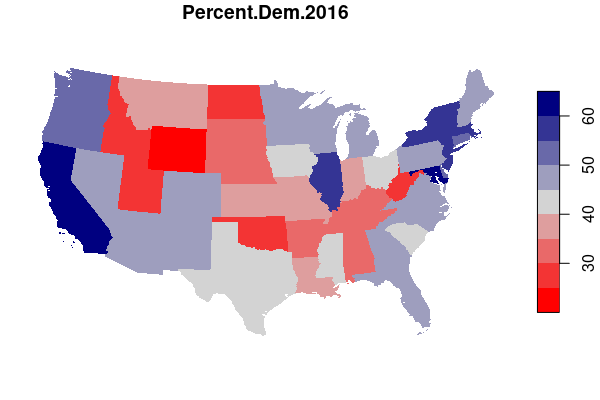
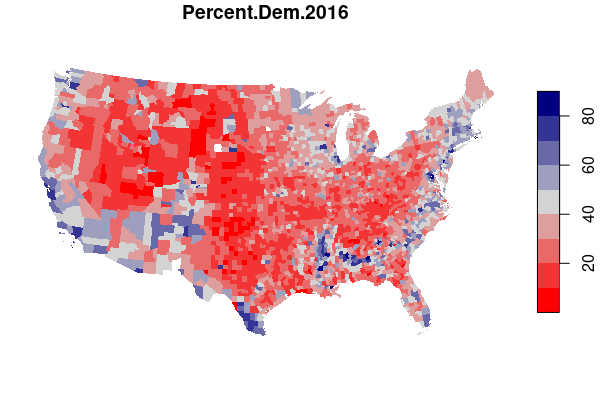
2016 percent Democratic presidential vote aggregated by state
2016 percent Democratic presidential vote aggregated by county

In drawing electoral boundaries, the MAUP is intentionally used in a process called gerrymandering, where specific groups of voters are either "packed" into a small number of homogeneous districts or "cracked" across multiple districts in order to reduce the power and representation available to those groups.

There is no universally applicable solution to the MAUP. In cases where accuracy is not essential (such as with data exploration) or possible (such as with data that has been aggregated for privacy reasons), the uncertainty presented by the MAUP may be acceptable as long as caveats are provided along with the analysis. In other cases, more-sophisticated analytical approaches may be more appropriate.

Selected Column Information

The following information on the variables selected above is from the BRFSS LLCP 2020 Codebook Report. If you use more-current data or other variables, you will want to consult the current codebook provided on the BRFSS website linked above.