World Map Projections
The Earth is a spheroid - it is round like a ball or sphere but flattened by slightly by the centrifugal force of rotation. The Earth has a circumference of around 24,900 miles, but is around 27 miles wider than it is tall.
The Earth exists in three-dimensions but, other than globes, most representations of the earth, such as maps, are two dimensional. A projection is a set of mathematical transformations used to represent the three-dimensional world in two dimensions.
This is a gallery of examples of notable projections used for mapping the world. For more details on these concepts and terms, see this tutorial on map projections. For even greater (albeit chaotic) detail, see Carlos Furuti's Cartographical Map Projections website.
Although the math behind projections can be quite complex and the distinctions between different projections in the same family can be subtle, world projections can usually be identified by:
- The shape of the outline of the map
- The spacing and curvature of the graticule (latitude and longitude) lines
- When graticule lines are not present, the distortions in the shapes of the countries
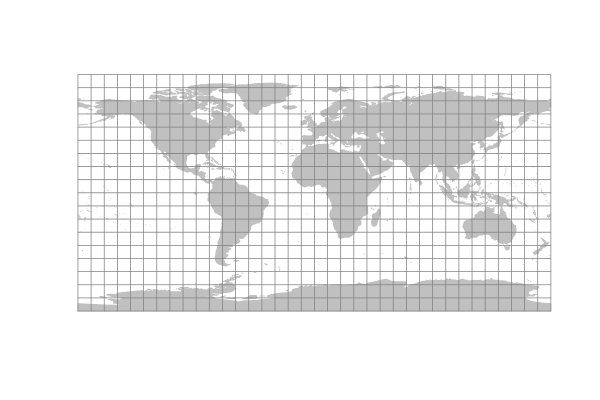
Equirectangular Projection
The simplest of all projections plots latitudes and longitudes as if the world were a grid of evenly spaced lines. Because longitude lines are physically closer together as you move closer to the poles, countries are distorted in width the further you move from the equator.
This projection should never be used in print maps as usage implies carelessness or ignorance of cartographic conventions. Desktop GIS software generally uses this as the default display for convenience.
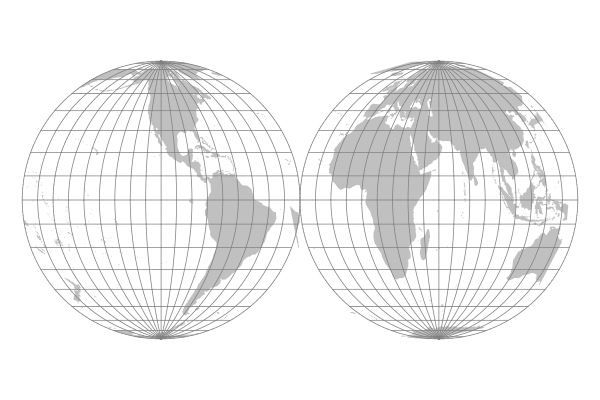
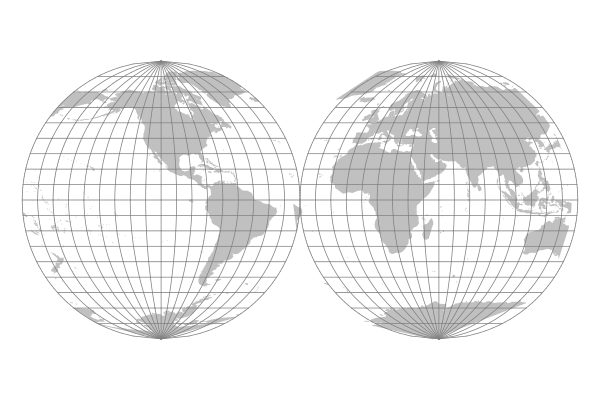
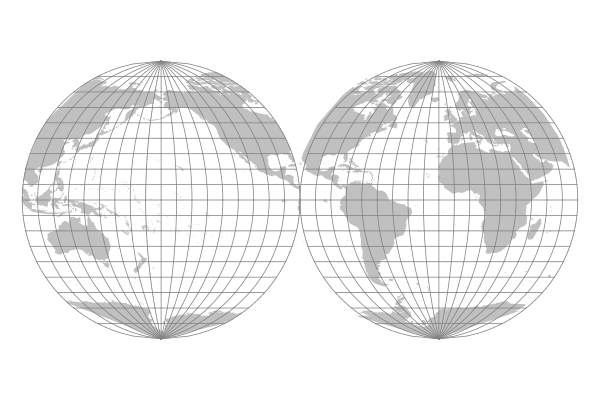
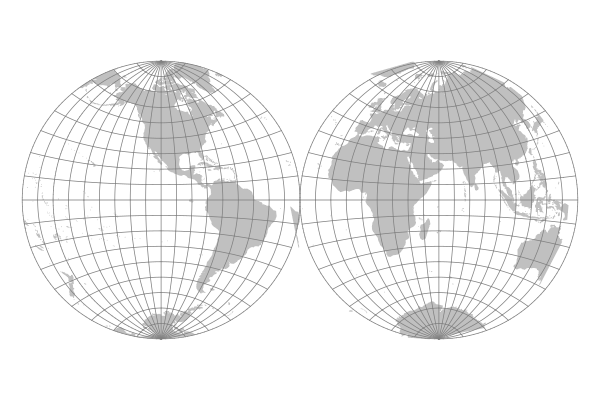
Globular Projections
Globular projections were once popular for wall maps, although they were supplanted in the 20th century by a variety of projections depicting the earth as a single flat surface.
Globular maps present a hemisphere of the Earth as if it were viewed as a globe. Two hemispheres are commonly presented side-by-side to cover the major land masses.
Although these projections appear quite similar on first glance, they each have distintive combinations of graticule line curvature and spacing.
Cylindrical Projections
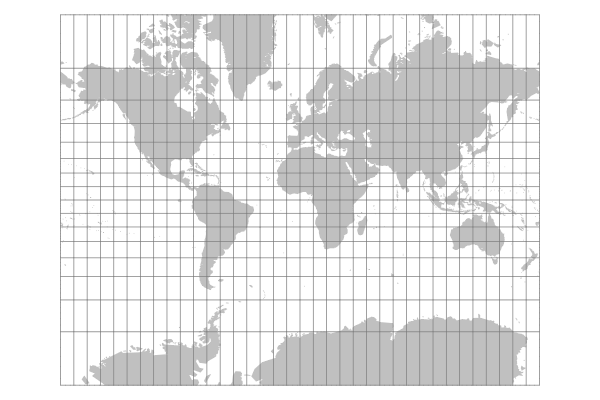
Mercator Projection
One of the oldest and most commonly-used projections was devised by the Flemish cartographer Gerardus Mercator (1512-1594) during the great age of European exploration. It preserved direction (conformal), making it useful for naval navigation.
Spherical Mercator
Spherical Mercator is a variant of Mercator that mathematically represents the world as a sphere rather than an ellipsoid to make calculations easier. This is the projection used by Google Maps and almost all other interactive web maps. The spherical representation causes inaccuracy when measuring large areas close to the poles, but is adequate for daily wayfinding and navigation in most of the world.
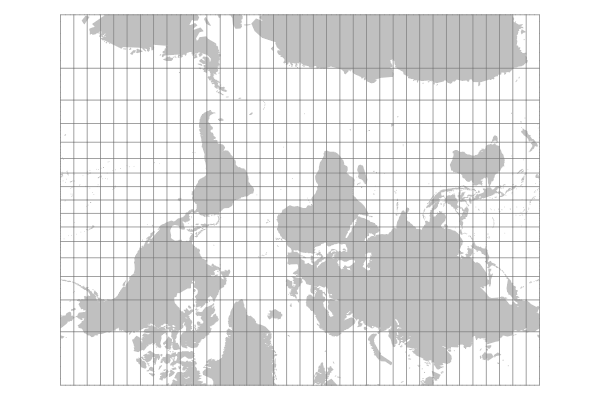
McArthur's Universal Corrective Map
There is no geological or astrophysical reason why North should be up on a map. This variant of the Mercator projection by Australian cartographer Stuart McArthur places south up to ask us to critically examine the biases inherent in the traditional north-up cartographic convention.
Azimuthal Projections
Azimuthal projections radiate outward from a single point (azimuth).
Although these projections resemble globular projections, note that globular projections only show a single hemisphere. Azimuthal projections cover the whole surface of the earth by wrapping the countries in the opposite hemisphere around the edges of the map.
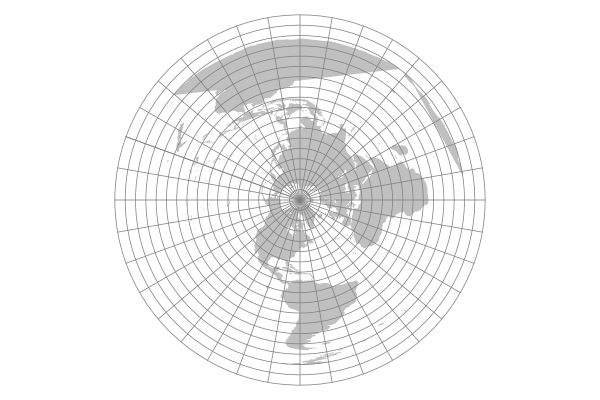
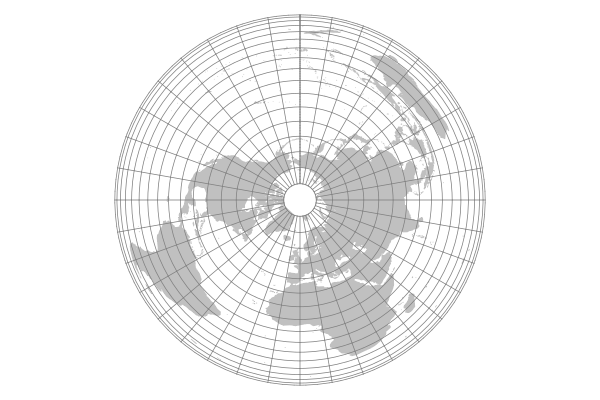
Azimuthal Equidistant
Azimuthal equidistant projections show true distances from a single point on the map.
Maps of the North and South Poles commonly use an azimuthal equidistant projection centered at the pole, although the center point can be anywhere on the planet.
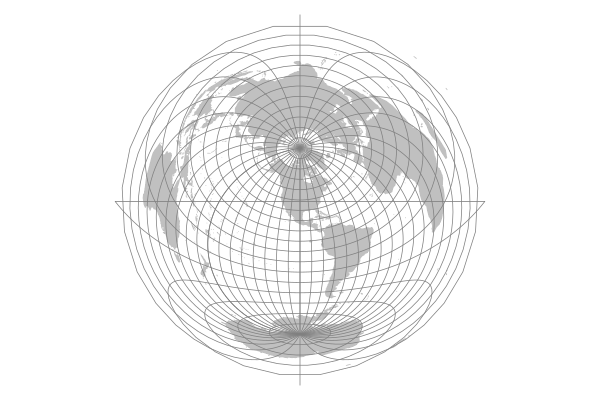
Azimuthal Equal-Area
The azimuthal equal-area projection was first presented by Johann H. Lambert in 1772.
Azimuthal equal-area projections are similar to azimuthal equidistant projections, except the radial lines get closer together as you get farther from the center point. This preserves area, but distorts distance and shape.
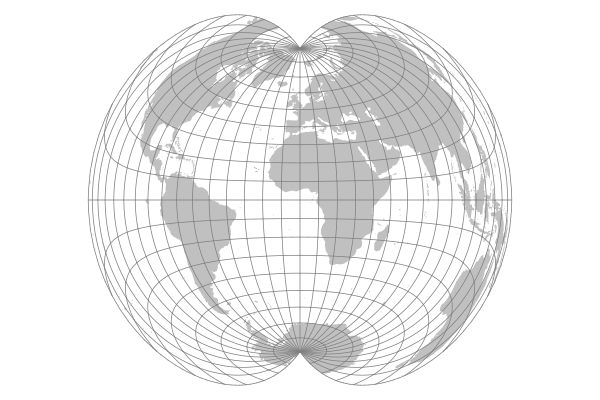
Azimuthal Conformal
Conformal projections preserve shape and angles at any single point on the surface of the earth.
The Lagrange projection is an azimuthal stereographic projection that was originally presented by Johann Heinrich Lambert in 1772 and generalized in 1779 by Joseph Louis Lagrange.
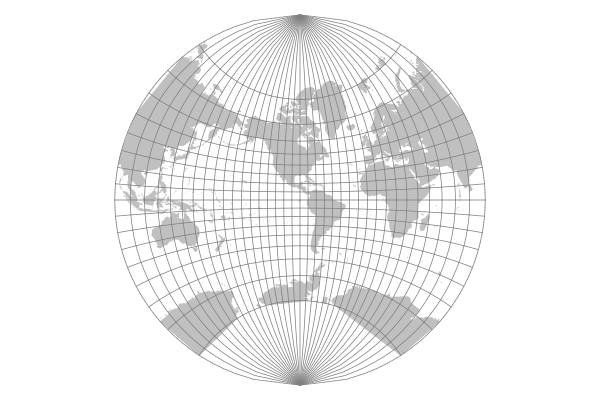
Modified Azimuthal Projections
Aitoff Projection
David Aitoff's projection from 1889 stretched an equatorial-aspect azimuthal equidistant projection into a 2:1 ellipse.
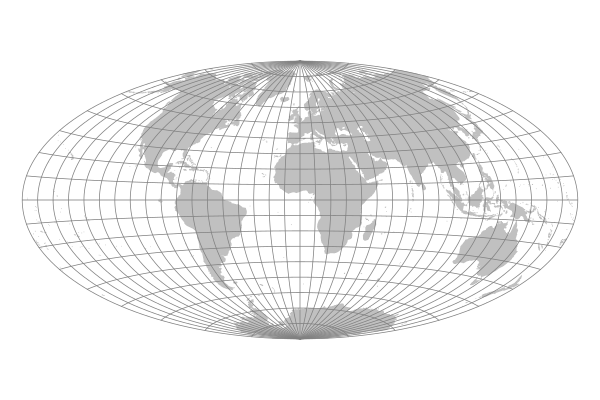
Hammer Projection
Ernst Hammer in 1892 applied the same stretching technique to an equatorial-aspect azimuthal equal-area projection.
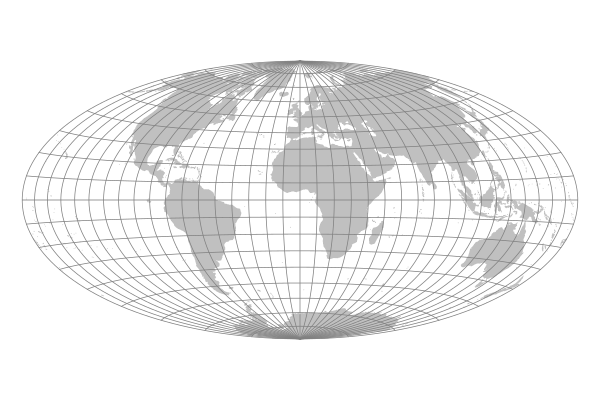
Briesemeister Projection
William Briesemeister in 1948 applied Hammer's technique to an oblique azimuthal equal-area projection with the center point at 45.0, -10.0, and an aspect ratio of 7:4.
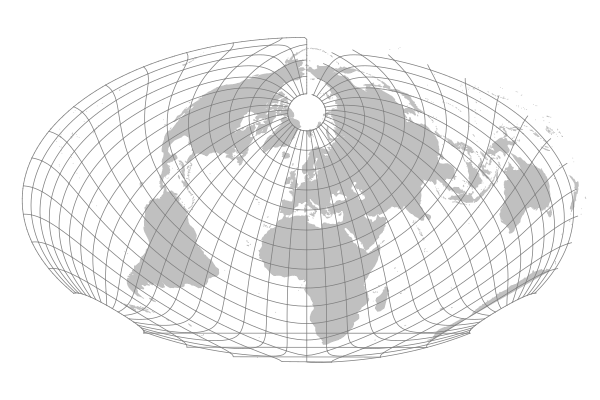
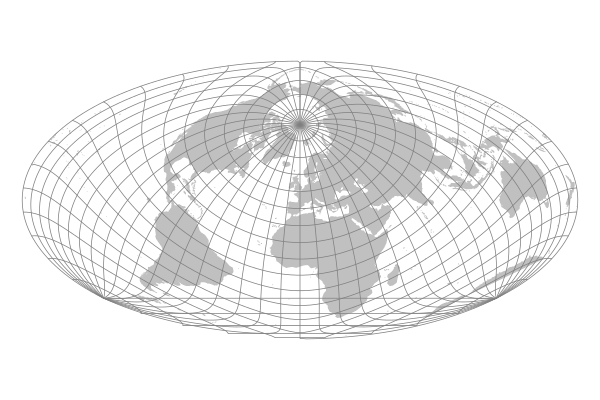
Nordic Projection
John Bartholomew's Nordic projection from 1950 rotated the azimuthal equal-area projection with 45.0, 0.0 as the central point before applying Hammer's technique, placing the Nordic countries at the center of the map.
Compromise Projections
Compromise projections distort area, distance, and direction in a variety of ways to achieve maps that permit a meaningful view of the earth in an aesthetically pleasing layout.
Robinson Projection
Arthur Robinson announced this projection in 1964. The Robinson projection solved the "Greenland Problem" by representing the country closer to its actual size than the Mercator projection. The Robinson projection is considered by many to be visually appealing and in 1988 was adopted by the National Geographic Society for some of its world maps in place of the older Van der Grinten projection.
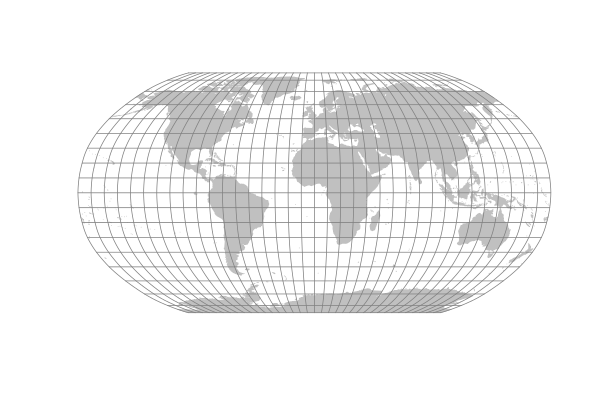
Winkel's Projections
Oswald Winkel announced a group of compromise projections in 1921. The most commonly known today is the Winkel Tripel.
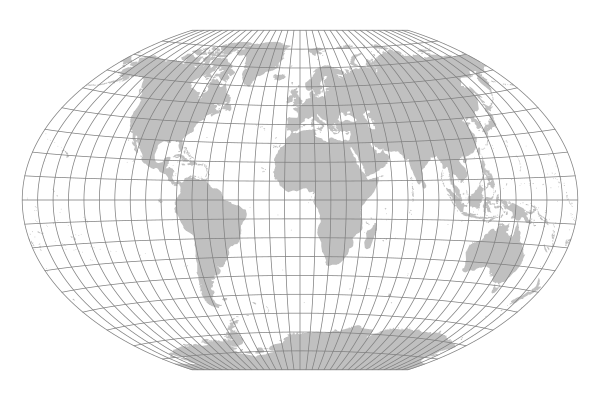
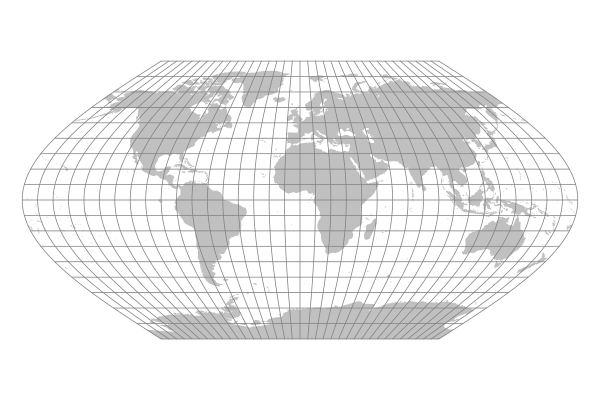
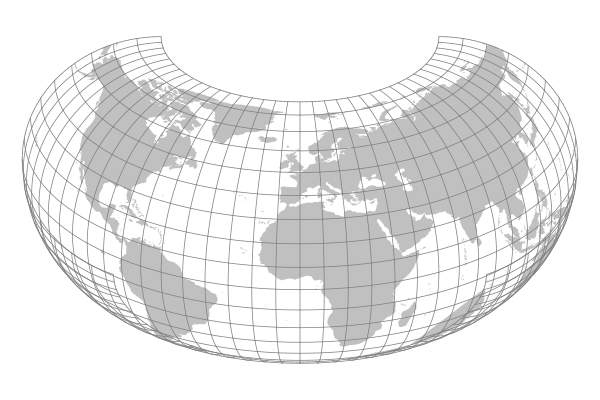
Raisz's Armadillo Projection
In 1943, Erwin Raisz announced a series of projections that utilized a variety of curved surfaces. Perhaps the best remembered is a projection on a torus that resembles an armored mammal common in the American South.
Interrupted Projections
Interrupted projections have gaps that minimize distortion of area and shape while avoiding breaks in land masses.
Goode Homolosine
John P. Goode produced this interrupted projection in 1923-25 and it was popular in 20th century atlases.
Fuller's Dymaxion
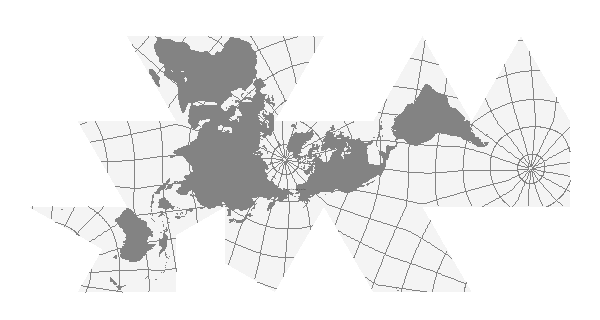
R. Buckminster Fuller was an American public intellectual in the early 20th century that had a fetish for triangles. His projection molded the globe into a isocahedron with 20 triangle-shaped faces. He then split the triangles in a way that created a flat map with Spaceship Earth as a continuous archipelago that aspired to break down the continental political barriers of his (and our) day.
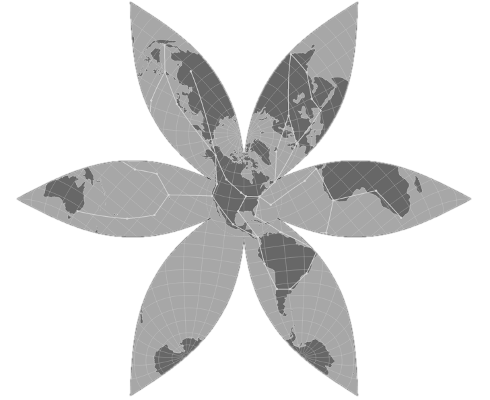
Gingery Projection
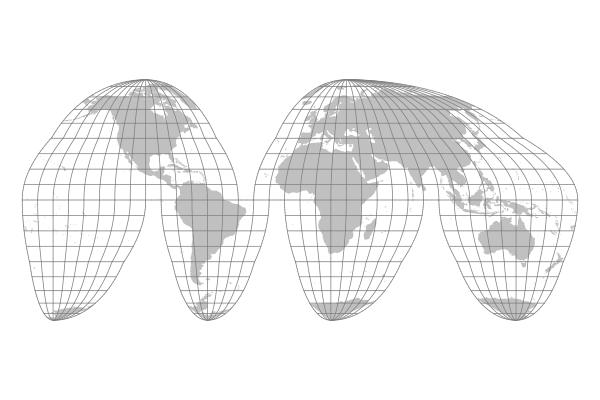
Walter G. Gingery's projection from June 1944 has an azimuthal equidistant projection at the center, surrounded by a six lunes that roughly align with the continents. The map is roughly equidistant but preserves shape, making it useful for rough distance calculation while still maintaining the shape of distant countries.
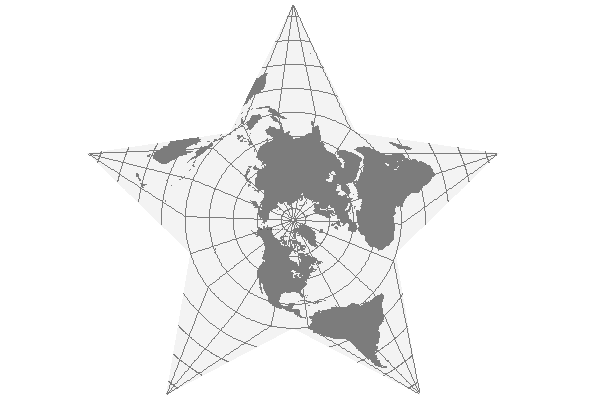
Berghaus Star
Hermann Berghaus' projection from 1879 is centered at the North Pole and breaks the earth into a five-pointed star. It was given an institutional foundation in 1911 when it became part of the logo for the professional organization that is now The American Association of Geographers.
R Code
Most of the diagrams in this tutorial were created in R using the sp, rgdal, and raster packages, with the world polygons from the maptools package.