Classification in ArcGIS Pro
ArcGIS Pro provides a number of different ways of allocating different ranges of numbers to different categories (classification methods). The choice of which method you should use depends both on the characteristics of the variable you are mapping as well as the story you are trying to tell.
The differences in the maps created with these different classification methods can sometimes be subtle, but can also be quite dramatic depending on the distribution of values in your variable.
This tutorial will walk through five steps to choose a classification scheme for a choropleth or graduated symbol map:
- Create the Map
- Analyze the Distribution
- Define the Audience and Intent
- Choose the Classification Scheme
- Publish
Create the Map
Classification is relevant primarily with choropleths (graduated colors), although it is also a lesser consideration for graduated symbols like bubble maps.
For this tutorial, we will use the Minn 2014-2018 ACS States feature service from the University of Illinois organization that contains a variety of useful variables from the American Community Survey. This data is also available as a GeoJSON file here.
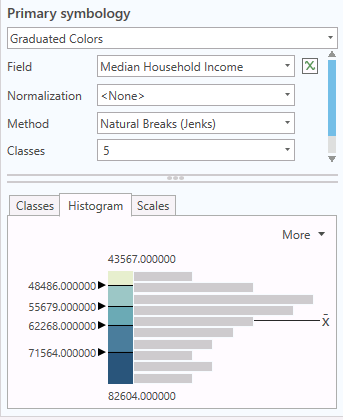
By default, this feature service opens with a display of median household income and an unclassed colors symbology, and the video shows how to change the classification to Natural Breaks (Jenks)
Analyze the Distribution
A distribution is the manner in which a variable's values are spread across the range of values. In ArcGIS Pro, the distribution of a variable you are symbolizing can be viewed in the histogram display on the classification dialog. The bars represent the number of features at different values, and those bars are overlaid by lines indicating where the active classification scheme draws the classification boundaries for colors / sizes.
The Normal Distribution
While there are dozens of mathematically-defined distributions that have a variety of applications in statistics, one very common distribution found in social and environmental geospatial data is the normal distribution (commonly called the "bell curve") where values are evenly distributed around a central value.
Skew
Perfectly normal distributions only occur in the abstract world of mathematics, and there are a variety of ways in which real-world distributions vary from the mathematical ideal. Those variations can guide the selection of classification schemes used to visualize your data.
One common variation is skew, where the clump of values is higher or lower than the middle of the range of values.
A good example is median household income, where most households clump around a middle range, but a handful of households have high or very high incomes, which skews the distribution to the right.
One extreme form of skew is the geometric distribution where values are clumped at the low end (left) of the distribution with a handful of high values spread out (skewed) to the right.
These types of distribution are common with population counts where a handful
of large areas/countries have high populations, but most areas are small and
have low populations. These are often log normal because the logarithms
of the values form a normal distribution.
Kurtosis
Kurtosis is the sharpness of the peak of a centralized distribution. If a distribution has a wide range of values and only a weak cluster around the central value, the kurtosis of that distribution is said to be low. If more of the values in the distribution are clustered around the mean than would be expected with a mathematical normal curve, kurtosis is said to be high.
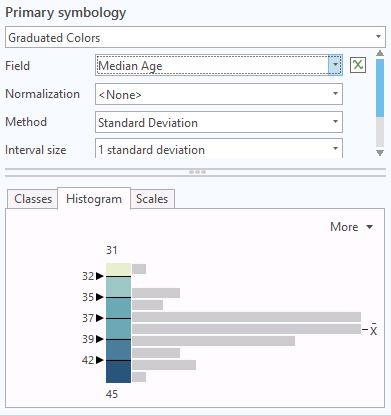
For example, although there are states with unusually high numbers of children (Utah) and unusually high numbers of seniors (Vermont), lifespans are fairly similar around the US, so median age by state has high kurtosis with a sharp peak around the average of 38.3.
An extreme example of low kurtosis is the uniform distribution, where values are spread fairly evenly across the range of values with no significant clusters.
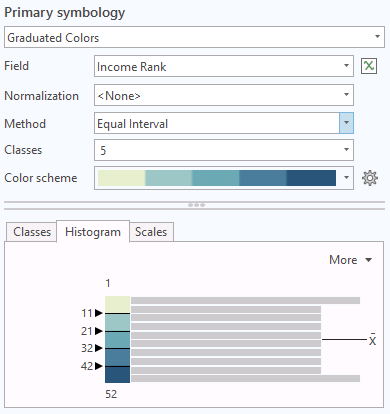
Uniform distributions are rare with social or environmental data. However, rank orders that force quantitative values into a sequence of ordinal numbers are uniform. For example, the distribution of the rank orders of percent of population that has a college degree is uniform.
Multimodality
Distributions often have multiple clumps of values. Even distributions with a dominant central clump may have smaller secondary clumps on the left or right tails. Such distribution with multiple clumps are called multimodal.
Most real-world geospatial data is at least a little bit lumpy. In evaluating these clumps, the question becomes whether those clumps represent something meaningful (such as a certain class of people or region of the country), or whether they are simply a random accident.
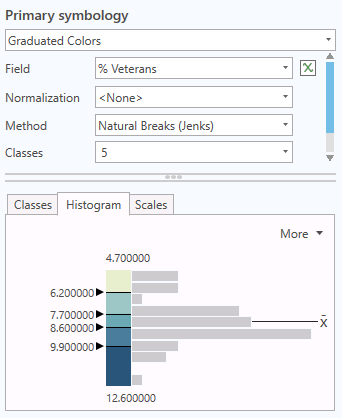
An example of a multimodal distribution is the percent of veterans by state. While there is a sharp peak (high kurtosis) around the mean of 8.2%, there is a smaller clump of states with low percentages (5% - 6%) of veterans.
Define the Audience and Intent
As with cartography in general, your choice of classification scheme will be influenced by the potential audience for the map, by their needs in reading the map, and by your intention for creating the map. While there are cartographic conventions that prescribe and proscribe certain practices, maps have different needs that can be met in different ways.
Toward that end, there are two broad considerations in choosing a classification scheme: understandability and focus.
Understandability
What information do you want users to be able to glean from the map?
You need to understand whether users will be using the map to find specific information about areas or simply need to get a general impression of the spatial distribution of the phenomena represented by the variable.
If users need to understand specific information, such as wanting to find the range of values for a specific city or county, the category boundaries should be clear memorable numbers where the user can understand their relationship.
If users are just using the map to get a general impression of where thing are, the boundaries can be determined by other aesthetic or ideological considerations.
Cartographic literature based on perceptual studies usually recommends five to nine classes as the maximum number of choropleth classes that map users can distinguish and comprehend (Declercq 1995, Mersey 1990). ArcGIS Pro usually defaults to five.
Focus
What information do you want to emphasize for readers of your map?
Different classification schemes will highlight the areas with the highest and/or lowest values, while others will create classes that cause a more uniform distribution of colors.
When your data is sharply skewed or has extreme outliers, you need to consider whether it is important to highlight those areas or to create a more even distribution of colors/sizes.
You need to decide whether you intend the classifications to represent clearly defined categories of areas (such as classes of income or levels of crime - low, medium, high), or whether they will simply be viewed relative to each other.
This is especially important with multimodal data. If the clumps represent important groupings that need to be accented, the clumps need to be in separate visual categories. However, if the clumps are just statistical accidents, emphasizing those clumps can create an impression of differences that the data does not support.
Choose the Classification Scheme
Natural Breaks (Jenks)
This scheme uses an algorithm to seek clumps of values that are clustered together in order to form categories that may reflect meaningful groupings of areas. It was named after the developer of the algorighm, George Jenks.
Natural breaks is the default in ArcGIS Pro and is a safe generic choice with most distributions if you are in a hurry and the map just needs to give a general impression of the distribution of values across the areas.
For the purposes of this tutorial, other classification schemes will be compared to natural breaks.
One problem can arise with natural breaks classification occurs when the data contains clusters of values that are not actually meaninful groupings. Natural breaks classification will place those clusters together and create a false visual impression that is not actually reflective of the phenomenon being visualized.
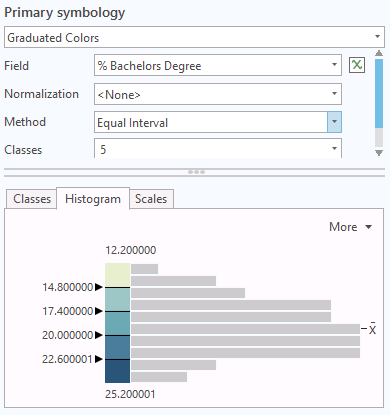
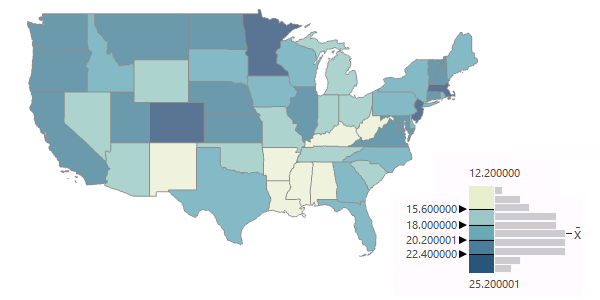
The example below is a map of the percentage of adults with bachelor's degrees by state. This variable has a normal distribution.
- Understandabiliy: Natural breaks maps can be hard to interpret because the class boundaries can fall on odd numbers that have no intuitive rationale. However, in this case, the normal distribution results in a fairly even set of intervals that are not particularly confusing.
- Focus: Because the distribution is normal and the breaks are fairly even, the map is visually balanced into five categories that do not seem to emphasize any one category or region.
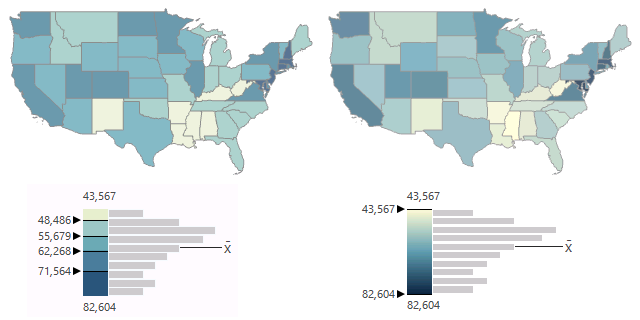
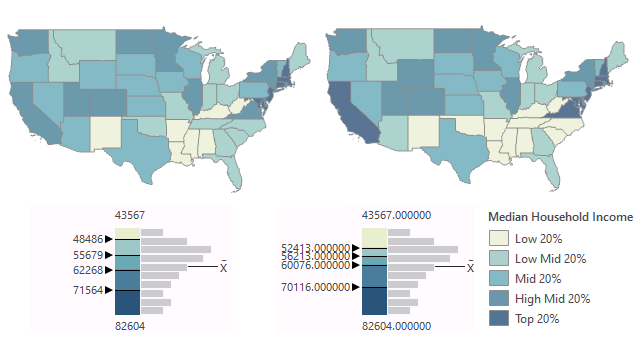
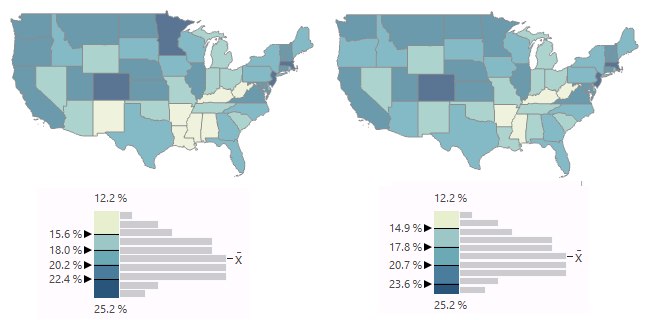
Quantile
Quantile classification creates grouping so that there are an even number of values in each grouping. This effectively creates a map showing the rank order of a variable. If you use the ArcGIS default of five categories, you are dividing the features into five ranked categories by percentile:
- Highest 20%
- High middle 20%
- Middle 20%
- Low middle 20%
- Low 20%
Assuming the areas are of comparatively similar size, quantile classification distributes the colors of a choropleth evenly across the map and can blur clusters that occur in the data.
This example is a map of median household income by state. This variable has a skewed normal distribution because most American households are clumped around the mean, but a handful of wealthy / expensive states extend the right tail of the curve.
- Understandability: Because the values for the breaks between classes are determined algorithmically, they will likely have no inherent meaning or purpose. However, if you modify the legend to describe the breaks in percentiles, the categories will be much more understandable.
- Focus: Compared to natural breaks, the quantile classification expands the numbers of states in the lowest and highest income and draws focus away from the states that are unusually poor or wealthy. Whether this is desirable is dependent on what you want the audience to take away from the map.
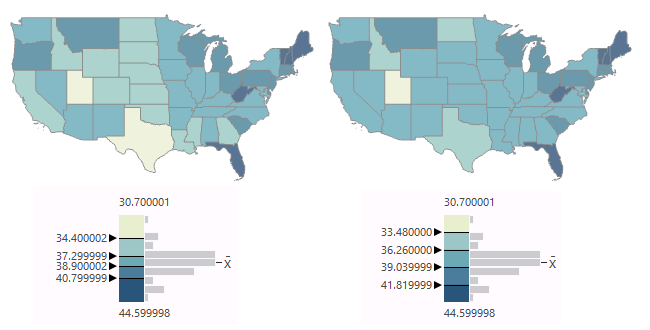
Equal Interval / Defined Interval
Equal interval classification divides the range of values evenly by the number of categories to create evenly spaced categories.
Defined interval classification is like equal interval except the cartographer can specify the numeric width of classes and the software will adjust the range and number of classes accordingly.
This example of median age has a distribution with high kurtosis.
- Understandability: Equal intervals are the easiest to interpret since there is a clear numeric pattern to the category boundaries.
- Focus: The equal interval classification with a normal distribution de-emphasizes the central cluster and brings out the extremes on the tails, as opposed to the natural breaks classification that brings out subtle variations in the middle that may not be meaningful.
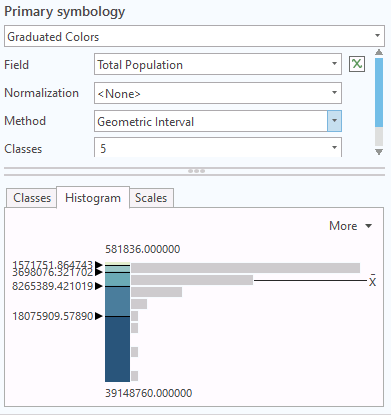
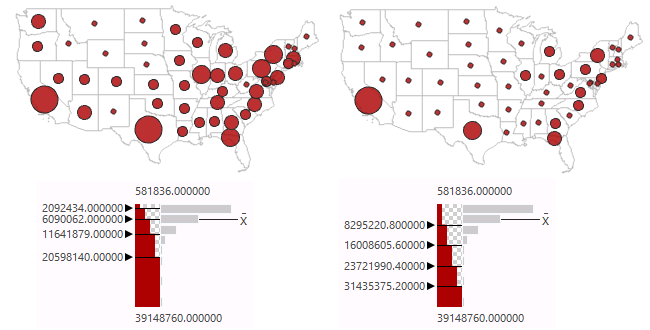
Likewise, for a map of population (highly skewed log-normal distribution) the equal interval classification clearly focuses on how much more highly-populated the largest states are relative to the country, as opposed to the natural breaks classification which creates aggregations that blur those distinctions.
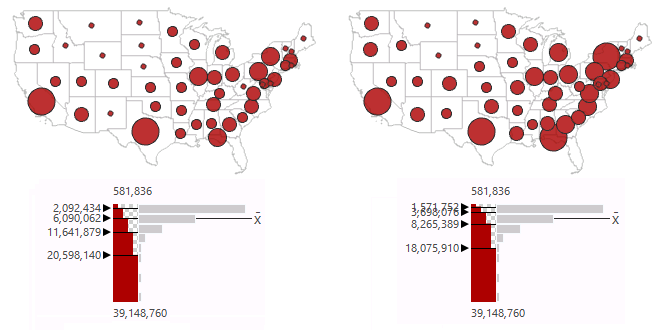
Geometric Division
Geometric classification performs an equal interval classification on a logarithmic scale. This scheme is most appropriate for data with a highly skewed log-normal distribution.
This example uses population of states.
- Understandability: A logarithmic scale should be clear to experienced map readers with some statistical knowledge, but it can be mystifying to people who do not understand logarithms.
- Focus: This scheme makes variations within the low value cluster to be visible in a way that they would not in an equal interval classification. It also avoids natural breaks potential for creating class breaks on statistical anomalies. However, the logarithmic compression of values de-emphasizes wide variations, which can be a drawback when that is something the cartographer wishes to communicate.
Standard Deviation
Standard deviation classification choses classes based on the mean and standard deviation.
This is the most statistically rigorous classification scheme, although it only has that rigor if used with data that is normally distributed. The algorithm does not transform to compensate for skew, kurtosis, or multimodality.
The example below is a map of the percentage of adults with bachelor's degrees by state. This variable has a normal distribution.
- Understandability: When creating maps for scientific audiences, this is a good choice when the data supports it. However, as with geometric classification, standard deviation classification will be mystifying to map viewers who do not have an understanding of basic statistics.
- Focus: Standard deviation classification calls attention to outliers and values in the extreme tails. However, that can result in aesthetically bland maps since those values are rare in normally-distributed data.
Continuous Color Scheme
You can avoid the pitfalls of classification by not classifying and just using a continuous color scheme. This is similar to equal interval classification, and you can use a logarithmic or exponential transformations if your data is heavily skewed.
- Understandability: Continuous classification should be used only when a general impression of the spatial distribution is desired, since users cannot clearly identify specific values or ranges of values based on colors that have such a wide variance. Use of transforms for skewed data will add additional mystification for inexperienced map readers.
- Focus: Because small color distinctions are not perceptible, continuous classification highlights extreme values while reducing feature contrast for the bulk of the values in the cluster(s). This can be good with normally-distributed data if your objective is to emphasize centrality, but is detrimental if you are trying to focus on differences in the middle of the range of values.