Preliminary Regression Analysis
Michael Minn - 23 March 2015
Variables
ZNDVIDIFF: Parcel pre-/post-foreclosure difference in NDVI deviation from tract median
ZASSESVALUE: Assessed value at time of foreclosure
ZHOMESQFT: Home square footage
ZHOMEAGE: Age of home at time of foreclosure
ZMEDHHINC: 2012 ACS median household income in census tract containing parcel
ZMEDIANAGE: 2012 ACS median age of residents in census tract containing parcel
ZPMEDPRE: Median parcel-level NDVI estimate one year prior to foreclosure
All variables were normalized to z-score before processing
The data is avilable for download as a zipped CSV HERE...
Linear Model
The following is a summary of a linear model with ZNDVIDIFF (NDVI difference in deviation) as the dependent variable and using QR factorization for least squares approximation.
While most of the variables are flagged as significant, the model fit is extremely poor (R2 = 0.014), as shown in the graph below.
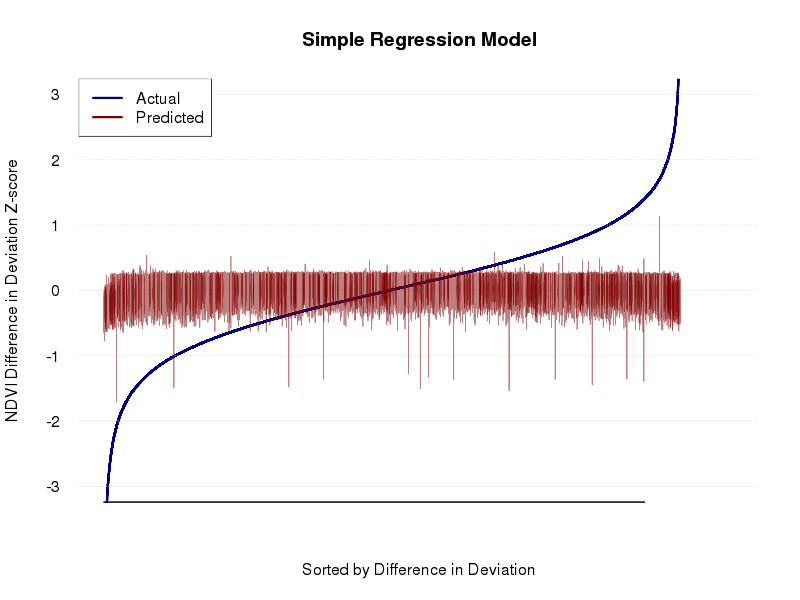
Call:
lm(formula = ZNDVIDIFF ~ ZASSESVALUE + ZHOMESQFT + ZHOMEAGE +
ZMEDHHINC + ZMEDIANAGE + ZPMEDPRE, data = foreclosures)
Residuals:
Min 1Q Median 3Q Max
-13.0331 -0.5687 -0.0142 0.5613 23.8114
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.035769 0.006667 -5.365 8.10e-08 ***
ZASSESVALUE 0.071671 0.013239 5.414 6.19e-08 ***
ZHOMESQFT 0.001032 0.031124 0.033 0.974
ZHOMEAGE -0.223564 0.035440 -6.308 2.83e-10 ***
ZMEDHHINC -0.026457 0.003363 -7.866 3.68e-15 ***
ZMEDIANAGE 0.003477 0.002924 1.189 0.234
ZPMEDPRE -0.115643 0.002566 -45.063 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9926 on 159503 degrees of freedom
(83128 observations deleted due to missingness)
Multiple R-squared: 0.01424, Adjusted R-squared: 0.0142
F-statistic: 384 on 6 and 159503 DF, p-value: < 2.2e-16
Probit Models
Probit models were built using with the sampled Google Earth observations of vegetation change (INCREASE and DECREASE) as the dependent variables.
In both cases, none of the provided variables were found to be significant, as shown in the summary below.
Call:
glm(formula = DECREASE ~ ZASSESVALUE + ZHOMESQFT + ZHOMEAGE +
ZMEDHHINC + ZMEDIANAGE + ZPMEDPRE, family = binomial(link = "probit"),
data = sample)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.3964 -0.6537 -0.5333 -0.3612 2.3093
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.24507 0.63362 -0.387 0.699
ZASSESVALUE 0.08499 0.76696 0.111 0.912
ZHOMESQFT 1.71773 1.76614 0.973 0.331
ZHOMEAGE 5.30920 3.40561 1.559 0.119
ZMEDHHINC 0.02243 0.20007 0.112 0.911
ZMEDIANAGE -0.04649 0.24648 -0.189 0.850
ZPMEDPRE 0.12789 0.10096 1.267 0.205
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 103.260 on 100 degrees of freedom
Residual deviance: 91.798 on 94 degrees of freedom
AIC: 105.8
Number of Fisher Scoring iterations: 5
===================================================
Call:
glm(formula = INCREASE ~ ZASSESVALUE + ZHOMESQFT + ZHOMEAGE +
ZMEDHHINC + ZMEDIANAGE + ZPMEDPRE, family = binomial(link = "probit"),
data = sample)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.3303 -0.4810 -0.3094 -0.1364 2.5999
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.12159 1.06155 -1.999 0.0457 *
ZASSESVALUE 0.71895 0.93249 0.771 0.4407
ZHOMESQFT 0.82453 2.26813 0.364 0.7162
ZHOMEAGE -4.63441 5.37619 -0.862 0.3887
ZMEDHHINC 0.05727 0.22800 0.251 0.8017
ZMEDIANAGE 0.06152 0.35986 0.171 0.8642
ZPMEDPRE -0.20513 0.14984 -1.369 0.1710
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 65.226 on 100 degrees of freedom
Residual deviance: 51.898 on 94 degrees of freedom
AIC: 65.898
Number of Fisher Scoring iterations: 7