Curving Grades With a Normal Distribution
This tutorial describes a technique for curving class grades using a normal curve.
The Normal Distribution
A distribution is the manner in which a set of values are distributed across a possible range of values.
Many human and environmental phenomena follow a normal distribution, The smoothed histogram associated with the normal distribution is popularly known as the bell curve. Examples include:
- Standardized test scores
- The heights and weights of frogs
- The heights and weights of people in the United States
- The deviations of actual weights of potato chips from the weights marked on the package
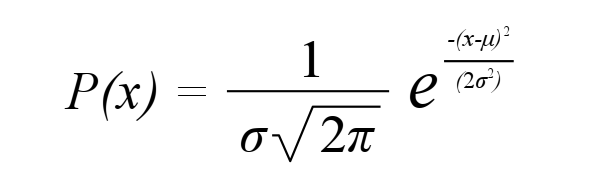
While the formula for the curve is ugly, the concept is fairly simple.
The bell curve is a density curve, where the x axis represents values from the distribution. The area under the bell curve between a set of values represents the percent of numbers in the distribution between those values.
The middle value of a normal distribution is the mean, commonly called the average value. The mean value is represented with the lower-case Greek letter mu (μ), which looks like an italicized lower-case English letter "u".
The width of the bell curve is specified by the standard deviation. Standard deviation is represented by the lower-case Greek letter sigma (σ), which looks like a lower-case English "b" that's had too much to drink.
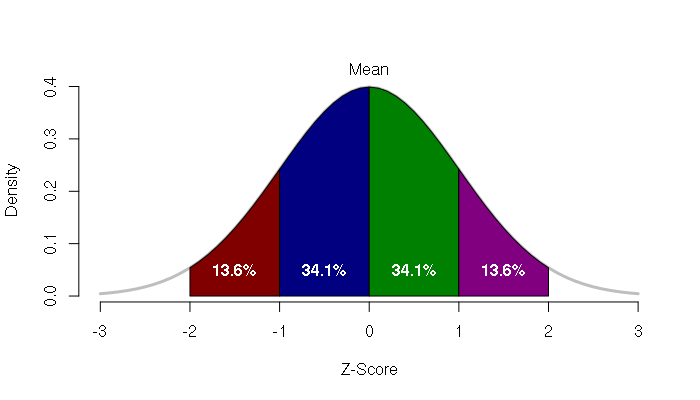
The number of standard deviations that a value departs from the mean is called the z-score. The z-score of the mean is zero. Converting values to z-scores is called standardizing.
The area under the bell curve between a pair of z-scores gives the percentage of things associated with that range range of values. For example, the area between one standard deviation below the mean and one standard deviation above the mean represents around 68.2 percent of the values.
Male Height Example
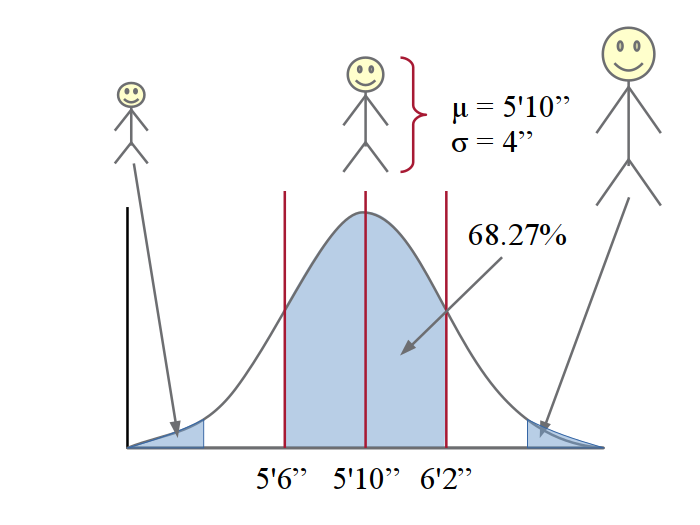
For example, in the USA the distribution of heights for men follows a normal distribution.
The average height for men in the US is around five feet, ten inches and the standard deviation is around four inches.
The number of very short men is the small area under the left tail of the bell curve, and the number of very tall men is the small area under the right tail of the bell curve. But most men are right in the middle around the mean.
68% of the distribution is within one standard deviation of the mean. So, 68% of American men are between five feet, six inches and six feet, 2 inches tall.
The name normal curve is related to the everyday concept of normal as conforming to a type, standard, or regular pattern. Mathematically, if you are right around the mean, you can be called normal.
Grade Distributions
In many school courses, the distribution of grades also roughly follows a normal curve. For example, this is a histogram of final point totals for a 28-person class.
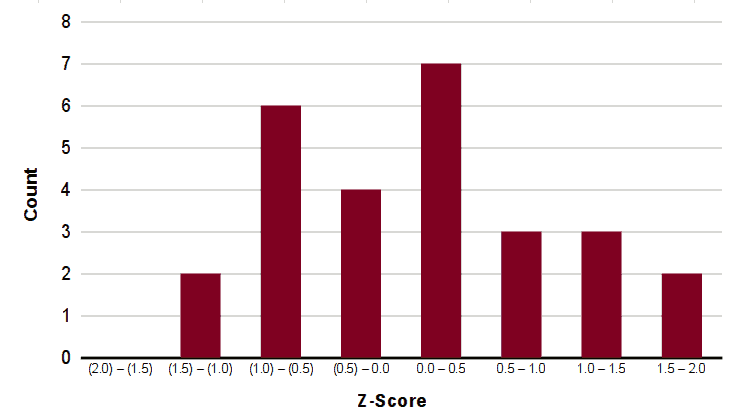
With small numbers of values, the normality of the distribution is not often obvious with a histogram.
However, if you take the integral of the normal curve, you get the cumulative area, which forms a sigmoid curve. This curve is often called an s-curve because it resembles an S. The X-axis is the grade, and the Y-axis is the percentage of the class.
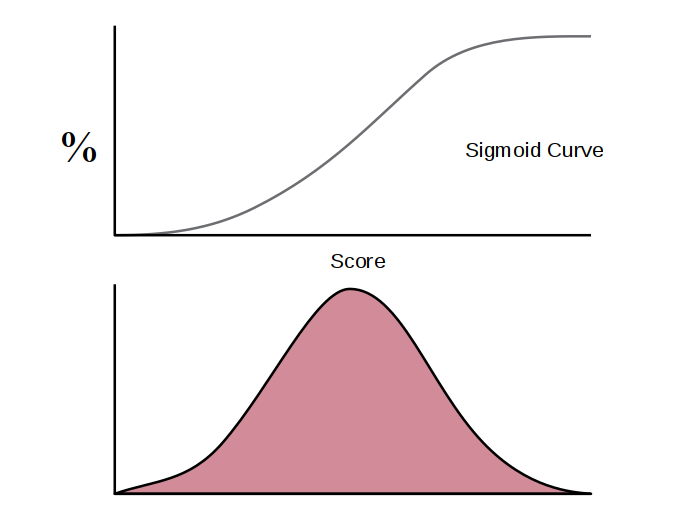
If you turn the curve on its side, you reverse those axes. The X-axis is the percentage of the class and the Y-axis is the grade. Each student represents a percent of the class. If there are 25 students, each student represents 4% of the class.
This means you can place bars under the S-curve by rank order with the score of each student. If the distribution of scores is normal, the bars will line up with the curve.
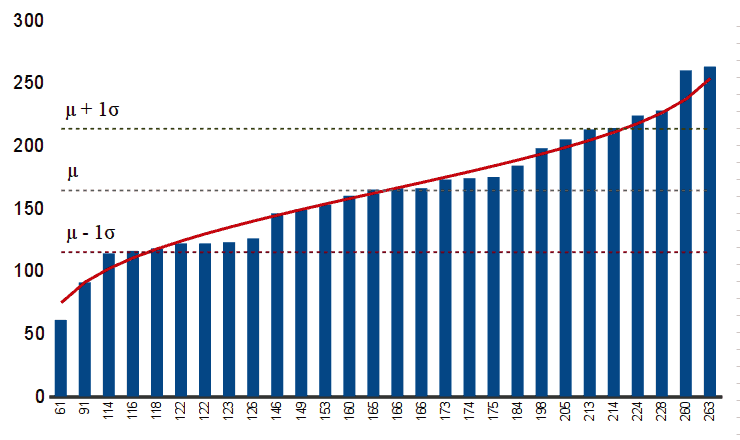
Given this mean and standard deviation, you can convert point totals to grades with a simple formula. For example, at an institution with a traditional percentage definition of letter grades, a typical formula that places the mean of the class at 85% representing a B letter grade and a standard deviation of 10% giving students one standard deviation or greater with an A letter grade:
μ = mean of all student point totals
σ = standard deviation of all student point totals
z = (student_point_total - μ) / σ
percentage = 85 + (10 * z)
The normal curve is an abstract mathematical ideal, and reality rarely exactly matches this ideal. So, the bars will rarely exactly line up with the curve. However, if they are close, you know you have a normal distribution, and this represents a useful technique for modeling and quantifying characteristics and performance.
Choosing Coefficients
While the normal curve is a fairly rigorous model, the choice of coefficients used to convert the z-score to the grading system at any particular institution is dependent on the norms of the institution and the extent to which a course is expected to be "hard" or "easy" relative to other classes.
For example, at an institution where 93% = 4.0, 83% = 3.0, etc., the 85% / 10% coefficients used above give a rough approximation of the GPAs within the student population, with slight stretching to represent an above-average level of course difficulty for this particular population.
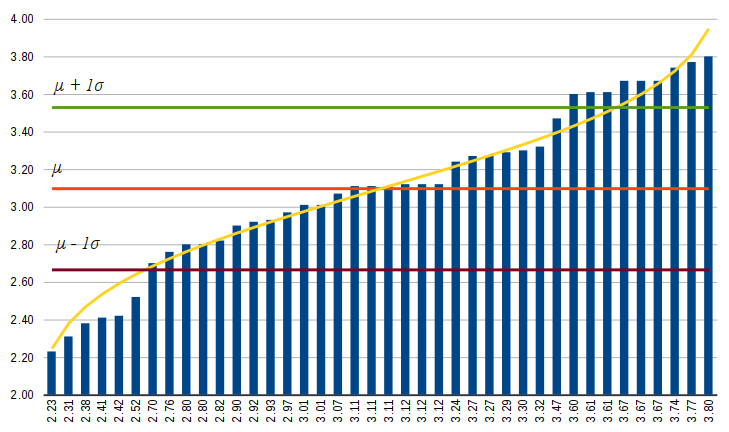
Change Over Time
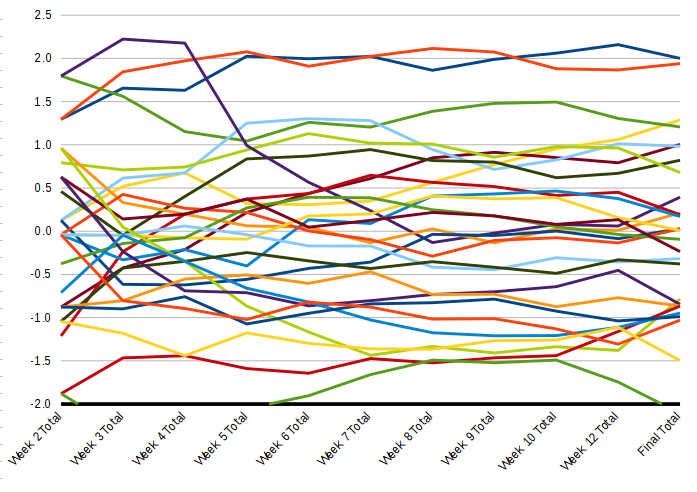
The performance of individuals over a semester can fluctuate widely, especially in cases of students who have to deal with particularly difficult personal challenges over the semester. However many students also stay within a surprising narrow range over the semester.
Critiques
The learning process is complex and no evaluation system can ever be considered perfect. The following are some critiques of curving and responses to those critiques.
Fairness
Some students may question whether it is fair to evaluate relative to other students in the class.
Because the grading formula is applied equally to all students, it is fair, although this does raise the question of whether a curve is appropriate for a given population and/or course topic.
In situations where there is a clear standard for what needs to be mastered to pass a course, curving may not be appropriate. Courses in the hard sciences or courses that involve specific professional skills are possible examples.
However, in non-critical situations like general education courses where the students often have extremely wide ranges of skills and engagement, grading normatively may be appropriate to avoid either failing large numbers of students, or giving high marks to students who are not high achievers within the norms of the institution.
Indeed, instructors commonly adjust assessments over the course of a semester to normalize the distribution of scores. Use of a curve simply moves this adjustment from assessment design to assessment calculation, shifting the focus from the metric to the material.
Effort
Students may express concern that their curved scores do not reflect the amount of effort put into a class. This is especially common with low-performing students who have not been held to high standards in the past, or who are seeking to leverage philosophical ambiguity into a scoring advantage.
It is, of course, difficult to quantify effort, especially when working with academically-diverse populations where some students will find mastery of the material requires little effort, and other students consistently struggle.
Use of a curve places the focus on performance. If a student has scores that are coming in below the norms of the class, the focus can then be shifted to what specifically that student needs to modify in their preparation to come up to the standards of the rest of the class.
Competition
The use of a curve turns class performance into a competitive zero-sum game. This has been observed as a disincentive to study, and can be a disincentive to the development of collaborative skills needed for most careers (Dubey and Geanakoplos 2016).
A similar dynamic has been observed in the professional world in the process of evaluating employees on a curve with stack ranking, where certain percentages of employees are given normally distributed rankings of excellent, acceptable, or poor regardless of absolute performance. This leads to a destructive focus on competition within the internal bureaucracy rather than an external focus on the core mission of the business. (Eichenwald 2012).
This critique may be especially valid in cases where collaboration is integral to the class procedures, or in honors classes where the standard deviation will often be small and curving would give low scores to students whose performance is only marginally different from their peers.
However, in situations like freshmen-level survey or general-education classes, where students largely function as independent agents, such competition may arguably be a realistic mirror of the real world, encouraging competitive, high-performing students to excel.
Discouragement
When working with low-performing students who often have low academic self-esteem, and/or multiple layers of extrinsic factors that have contributed to low performance, curving creates a positive feedback loop that can reinforce poor self-image and lead to discouragement.
This critique will have different levels of seriousness depending on the population of an institution and the broader social justice mission of the institution.
The draconian argument is that education is part of a social filtering process where students are sorted into life paths appropriate to their capabilities.
However, this could again be translated into a renewed focus on the material and performance rather than the metric. Because curving turns scoring into a mechanistic process, the focus can be turned to what caused the scores to be low relative to peers, and on how those issues can be addressed to improve performance. This requires individual initiative and attention on the part of both the student and the instructor, and may not be practical in situations with high workloads and student-teacher ratios.